--Thanks to all the creators especially Clowwindy!

概述

在阅读了shadowsocks的源码中，我学习到了以下几部分重要内容，包括且不限于：

1. 基于事件编程的编程模式及回调函数的概念和应用
2. 网络编程的I/O模型-特别是 I/O 多路复用的Reactor反应器模型
3. 守护进程的处理
4. 配置文件的读取及处理
5. 进一步了解了加密算法 将之前看过的密码学概述[^1]与实际应用相结合
6. 加深理解了代理服务器的概念
7. 对数据结构的初窥门径
8. 超时事件的处理

数据加密的理解

这部分我想按照从总结[^1]学到的知识体系出发，说明常规加密方法的目的和手段；再步入到早期Shadowsocks的加密需求，对其应用流加密（Stream Cipher）进行概述（现已废弃）；从而对Shadowsocks2.9.1的源代码中封装Stream Cipher进行简要分析；最后记录一下阅读NIST SP 800-38D[^2]和Shadowsocks SIP022[^3]的心得体会，具体说明基于gcm加密的操作方式以及在Shadowsocks中的应用（无代码，纯分析和臆想）。

计算机网络中对安全的需求与常用方法

首先，我要再次特别感谢《Computer Networking: a Top-Down Approach, 7th Edition》的作者：James F. Kurose和Keith W. Ross，中文版的译者：陈鸣，以及图书提供的线上材料[^4]，这一节的相关总结均直接或间接来源于丛书和线上材料。

这里需要说明的是，加密是在安全性要求的真子集中，实现机密性只是做到了一定程度的对通信安全的保证。

安全的特性

• 机密性（confidentiality）：这指的是信息的机密性质，即只有发送者和预期的接收者应该能够理解消息的内容，其他人无法轻易获取或理解其中的信息。这需要报文在一定程度上进行加密（encrypted）。发件人加密消息，接收者解密消息。
• 报文完整性（message integrity）：发送者和接收者希望确保消息在传输过程中或之后没有被篡改，且能够检测到任何篡改行为。
• 鉴别性（authentication）：发送者和接收者希望确认彼此的身份。
• 访问与可用性（access and availability）：服务必须对用户可访问且可用。

这里前三点是我们在Shadowsocks的设计中需要注意的，在早期的Shadowsocks的设计中，着重强调机密性；而后一些新问题的出现[^5]，对报文完整性和鉴别性提出了新的要求，而后对协议进行了修正。

在互联网通信中，存在诸多场景，只部分实现以上特性（IPSec 协议（仅加密模式）），甚至完全没有实现（HTTP的明文传输）。

为了易于理解，我们对前三个特性做一个简要的例子以方便理解：当你和朋友书信沟通时，书信用“火星文”完成，以让你的家长看不懂，这一定程度实现了机密性；在你收到对方的书信时，对对光查看有没有涂改痕迹，以确保你的家长没有偷偷修改你们的通信内容，这一定程度实现了报文完整性；在通信时，你们约定要用自己刻的某处有微小瑕疵的印章盖章，收到对方来信时，要查看这个印迹是不是对方独一无二的印章加盖出来的，这一定程度实现了鉴别性。也就是别人看不懂、没有被别人改以及确定是对方发的三个要点。

异或 XOR ⊕ 的运算基本规则

异或（XOR）是一种逻辑运算，通常用于比特（二进制位）操作。它的运算规则非常简单，其结果取决于两个输入的不同性。具体来说，XOR 的规则如下：

1. 当两个输入相同时，XOR 的结果为 0。
2. 当两个输入不同时，XOR 的结果为 1。

可以用以下真值表来表示 XOR 的运算规则：

输入 A	输入 B	A XOR B
0	0	0
0	1	1
1	0	1
1	1	0

符号 ⊕ 通常表示异或运算。例如，A ⊕ B 表示 A XOR B。

实质上，XOR可以看作二进制数据的一种加法和减法。这是一种模2算术，在加法中不进位，在减法中不借位。模2算术按我个人理解，就是两个比特串按对应位进行运算，加法和减法的结果都要mod 2作为这一位的最终结果。比如，11 + 01 时，左边第一位的结果是1+0 mod 2 =1，第二位结果是1+1 mod 2 =0，最终结果是10；11-01也是类似，左边第一位的结果是1-0 mod 2 =1，第二位结果是1-1 mod 2 =0，最终结果是10。

这意味着加法和减法是相同的，而且这两种操作等价于操作数的按位异或（XOR）。举例来说：

1011 XOR 0101 =1110

1001 XOR 1101 =0100

也就是

1011 - 0101 = 1110

1001 - 1101 = 0100

1011 + 0101 = 1110

1001 + 1101 = 0100

除了所需的加法或减法操作没有进位或借位外，乘法和除法与在二进制算术中是相同 的。如在通常的二进制算术中那样，乘以2就是以一种比特模式左移一个位置。

在理解了XOR可以作为一种加法（减法）的概念后，理解后面加密操作模式的一些操作就很简单了。这里值得深入记录的是，这里的加法和减法，实际上是有限域（GF，Galois Field）中的加法和减法。这里的Galois也是GCM操作模式的G。在 GF(2) 中，1 + 1 = 0，0 + 0 = 0，1 + 0 = 1，0 + 1 = 1。

下面是一些对应关系：

• 0 ⊕ 0 = 0 （GF(2) 中的加法 0 + 0 = 0）
• 0 ⊕ 1 = 1 （GF(2) 中的加法 0 + 1 = 1）
• 1 ⊕ 0 = 1 （GF(2) 中的加法 1 + 0 = 1）
• 1 ⊕ 1 = 0 （GF(2) 中的加法 1 + 1 = 0）

在GF(2^m)域中的乘法运算，可以参考[^14]，14中的例子本原多项式错了，没有x^2，是x，点进去看的请注意。计算时将GF(2^m)的元素作为多项式，在处理不属于GF(2^m)域的高次多项式时，通过本原多项式完成降阶，最终得到属于GF(2^m)的结果。对于Galois的运算和性质，还在了解过程中，现在摘两页书ppt放在这里先。

按照我个人的理解GF(2^m)域应该是构成一个阿贝尔群 (GF(2^m), +)，不过这是高中时候看的人教版数学选修3-4：对称与群。当时锤子没看懂，刚刚写博客时又翻了翻，发现里面还有伽罗瓦理论....我当时都没看到那儿...

看GF域相关的知识时，我又深感到了自己水平之低下....以前花了不少时间看概率论中的测度空间，看了许久就理解了基础定义，写大论文时候瞎几把胡诌上去了个自己理解的体系。上课时的泛函分析，张量分析，可以说基本没搞懂.....很多概念，往后深挖一步都是浩大的数学理论，但是非常遗憾的是，我并没有跨入的资格....每逢这种时候，深感挫败与无力。

虽然多年的积累，多多少少有点用处，高中时翻的选修4-6让我对模运算比较熟悉，能直接上手推一些基本的公式；选修4-9的马尔可夫链，直到硕士期间使用师兄的MCMC抽样程序时，也多少明白点概念。但是终究只有概念，不能深入理解其内涵。希望自己再过十年二十年，能稍稍的有自信的说出我入门了。也许像天赋有限的我，随着时间的积累，也能结出像样的果子吧。

确保安全的常用方法

• 对称密钥密码（Symmetric key cryptography）体制（DES、AES等）
• 公开密钥密码（Public Key Cryptography）体制（RSA等）
• 散列函数（Hash function algorithms）（SHA-1、MD5等）
• 报文鉴别码（Message Authentication Code，MAC）
• 数字签名及公钥认证
• 不重数（nonce）

对称密钥密码

对称密钥密码体制用于加密和解密通信中的数据，其中发送方和接收方共享相同的密钥。对称加密方式加密解密速度快，适合于大量要加密的数据，也就是Shadowsocks这种全程数据流都要加密的方式，因此这也是Shadowsocks主要采用的加密模式。

对称加密的最广泛应用的是AES（Advanced Encryption Standard），这是一个国际性的加密标准，得到了全球范围的广泛应用，可以通过AES指令集或AES指令扩展，对专门的硬件来优化和加速AES加密和解密操作。我在学习过程中，主要关注的aes-256-cfb和aes-256-gcm前者的aes就是这个对称加密方法。

AES（Advanced Encryption Standard）是一种块加密算法，有如下几个要点：

1. 块加密算法： AES将待加密的数据分成固定大小的块进行处理，每个块大小为128比特（bits）。
2. 每次操作处理一个完整的块： 在AES操作中，每次处理一个完整的块，而不是按位逐个操作。每个块的大小为128比特，整个过程以块为单位进行。
3. 按照一定顺序更替或打乱： 在每一轮AES操作中，通过一系列的替代、置换和混淆操作，如SubBytes、ShiftRows、MixColumns和AddRoundKey等，对块内的数据进行按照一定顺序的更替或打乱。实际实现中可以转换为查表操作([^7]中的Optimization of the cipher），以提升加解密的效率。
4. AES支持128、192和256的密钥长度，分别对应于10、12和14轮操作。而且密钥（Key）用于生成RoundKey，在每一轮操作中的AddRoundKey环节处理中间数据，这保证了使用不同的Key加密相同的数据可以得到不同的加密结果。

因为密钥长度越短，操作轮数越少，加解密消耗越少，所以在需要保证大吞吐量的情况下，可以优先采用128位的密钥长度。这印证了我用的机场采取aes-128的方式，而不是aes-256，也算是一个收获。

将按照一定顺序更替或打乱说的详细一点，以128位密钥为例[^6]，一共有十轮操作：

• 初始轮（1）
  • AddRoundKey
• 中间轮（2~9）
  • SubBytes：将数据块中的数据，映射到 Rijndael S-box，主要为了消除特征
  • ShiftRows：将数据块按“行”移位，以达到混淆的目的
  • MixColumns：将数据块按“列”与一个由多项式构成的 matrix，做矩阵乘法。目的是将单个错误扩散到整体，从而达到雪崩效应的预期，使其更难被破解
  • AddRoundKey：将本轮的 key 与数据块相加，由于使用 Galois field，在代码中只是一个简单的 XOR
• 最终轮（10）
  • SubBytes
  • ShiftRows
  • AddRoundKey

具体的有兴趣请自行查阅相关资料，这里做一个概述，以说明在应用AES时，Shadowsocks大体上是如何操作将明文转换为密文的，其中。

对称密钥密码与操作模式的结合

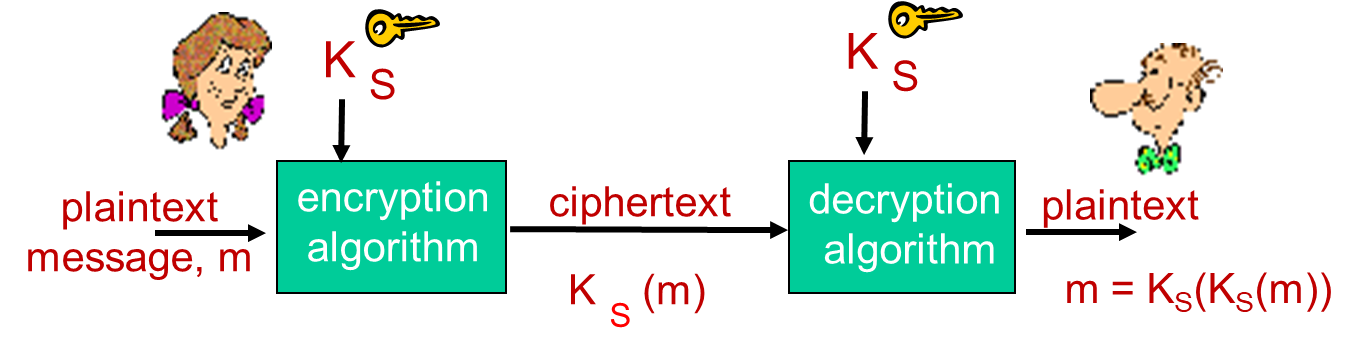
而与AES并行存在的，有一系列的操作模式。这二者的结合，可以使得一个仅用于机密性的块加密算法：可以有更好的机密性（ Cipher Block Chaining，CBC、Counter，CTR）；可以从块加密转换为流加密（Stream Cipher，即不按128比特加密，可以逐比特加密，随到随加密，随到随解密）模式（Cipher Feedback，CFB）；可以用于增强的机密性、完整性、鉴别性（Galois/Counter Mode，GCM）。

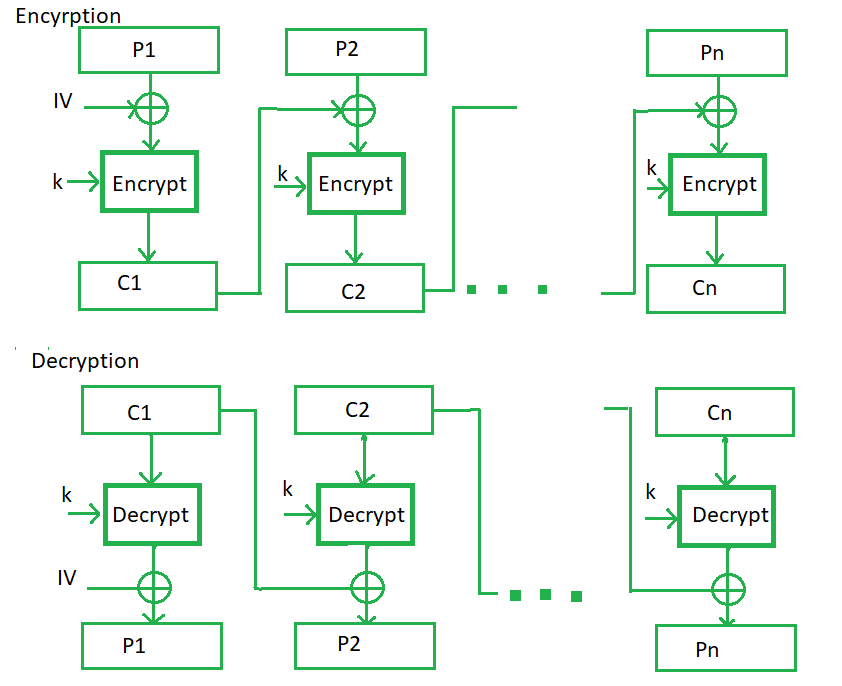
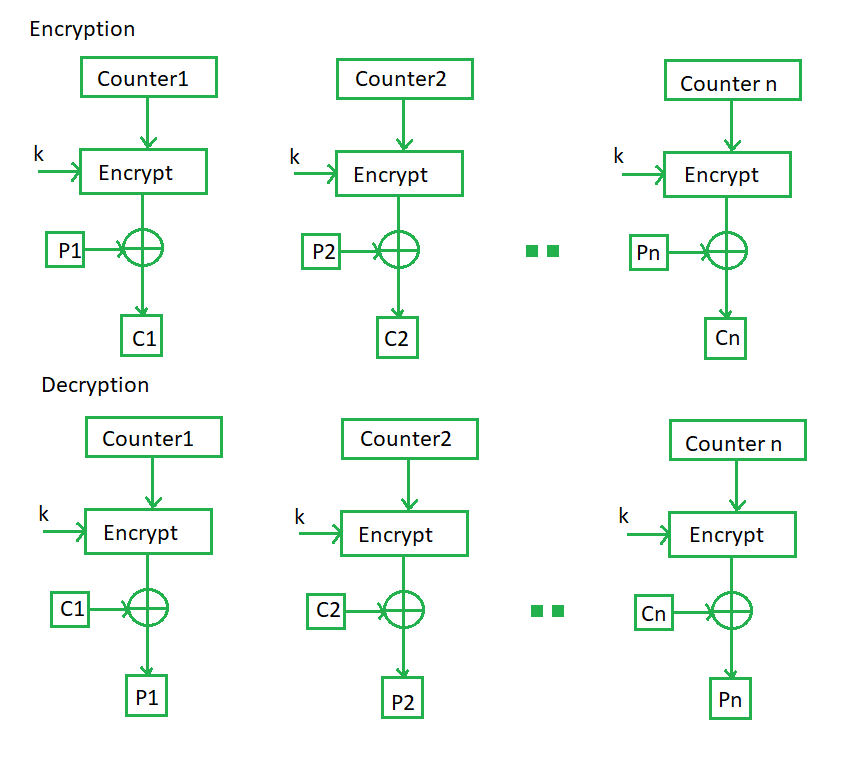
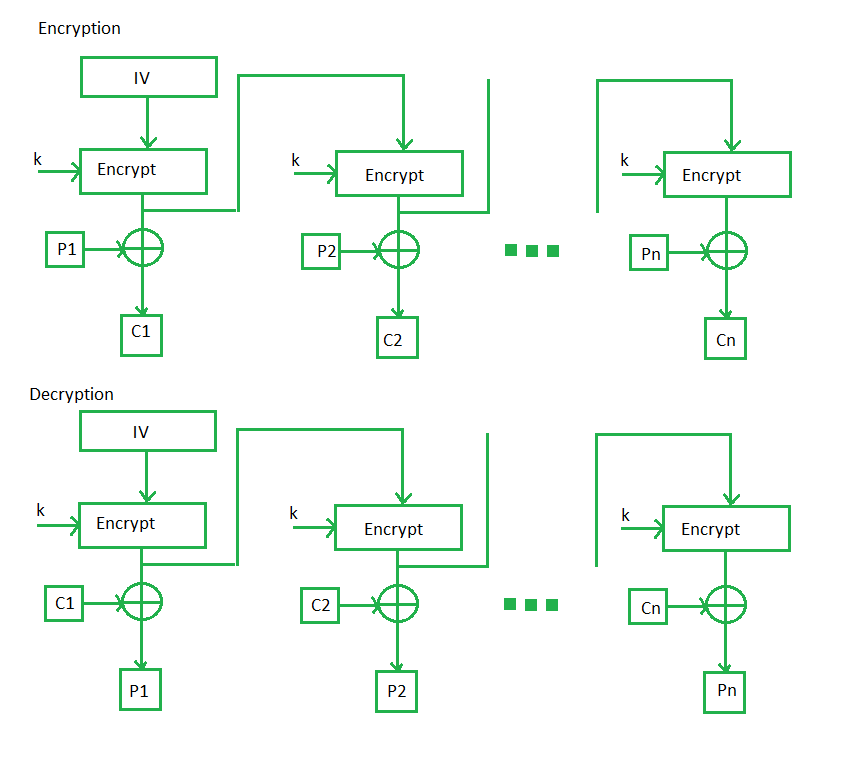
这里仅简单描述概念，详细资料请查阅相关资料，下方图片来源[^8]，其中的Encrypt和Deceypt可以是AES。

Cipher Block Chaining模式-基于初始向量，阻止同一明文块加密出相同密文

由上文描述可知，AES对每块的操作方法是一致的，因此在加密同样一个块时，会得到同样的结果。为了解决该问题，一种策略就是引入随机性。在CBC模式中，初始向量（Initial Vector，IV）被引入，IV是随机生成的。在加密每一个块时，会先将这个块与上一个块加密后的密文进行异或（XOR）运算，而后再加密；而在加密第一个块时，会将第一块明文和初始向量进行XOR运算。这样，加密同一个数据流，使用不同的IV就会得到完全不同的结果。解密是逆过程，按序解密再与对应的块取XOR操作即可得到明文。

Counter模式-基于计数器，阻止同一明文块加密出相同密文

与CBC不同，CTR使用了一个计数块（Counter）作为类似于CBC中IV的作用，它可以由0开始，也可以由随机数生成，但是在加密每一个块后，需要递增1，转换为Counter2，这样，在一次加密中，相同的明文块也会得到不同的密文块；但是Counter起始一样，对同一个数据流加密，会得到一样的结果，所以Counter的生成最好不要直接从0开始，而要采用一些生成方法。此外，CTR还是一种类似于Output Feedback Mode（OFB）加密模式，也就是说它是对CTR后加密后，与明文XOR得到密文，而不是将明文与Counter在XOR后的结果用于加密。OFB的概述在下一节给出。CTR通过计数块实质上产生了一系列的密钥流，这使得CTR可以作为流密码使用，类似于OFB。

Output Feedback Mode模式-调用底层加解密方法（如AES）时，只需加密方法

OFB在引入随机性时，也使用了IV。但其在加密解密时，均只用Encrypt方法，这是该方法的一个特点。OFB通过对IV进行多次加密，每次加密后的结果作为下一部分的密钥块，最终得到了密钥流。在密钥流与明文XOR运算后，得到密文。这里值得注意的是，OFB的出现，使得将AES从块加密方法转换为流加密方法成为了可能：我们得到了密钥流，就可以用密钥流去加密任意长度的原始明文。比方说生成了3个128比特的密钥流，第一次要加密270比特的数据，就可以从384比特的密钥流中，取出270比特；在又到达30比特数据时，就可以用第271-第300比特密钥流进行加密，而不需要对原始的明文进行任何的填充。但是流加密会造成明文和密文字节的一一对应，而一定程度丧失了AES在块内多次操作打乱的效果，从而更易造成密文被篡改的攻击。Shadowsocks就出现过这个漏洞，详情可以见[^5]，有兴趣的请自行查阅。

这里值得一提为何只需要加密模块即可完成加密和解密：KEY+明文=密文，密文-KEY=明文；之前有说过XOR可以看作加法和减法，二者是一致的，都是XOR运算，最终得到KEY XOR 明文=密文，KEY XOR 密文=明文。只要知道密钥流即可完成加密和解密操作。

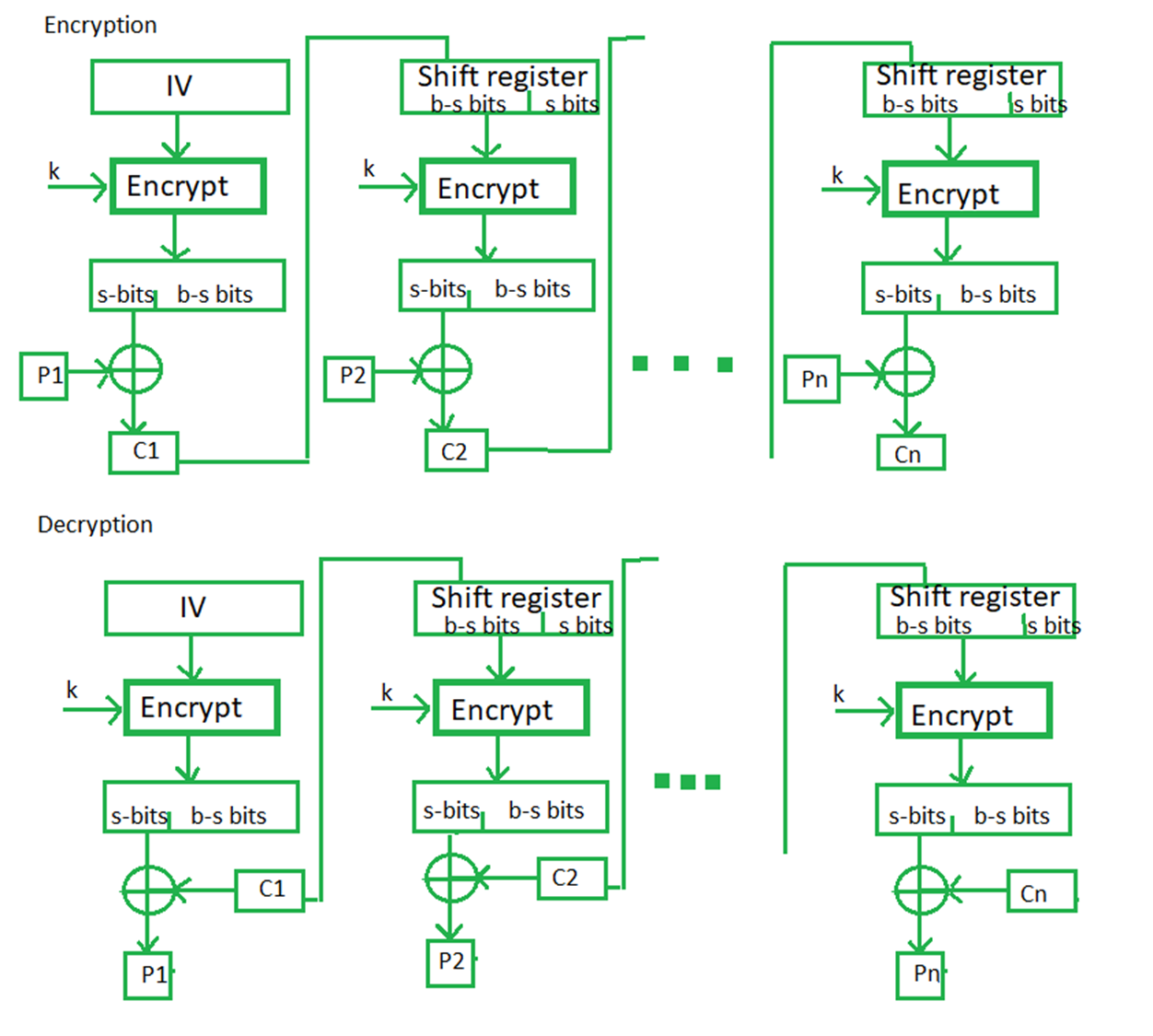
Cipher Feedback Mode模式-借鉴CBC和OFB的想法，提供了一种流加密的方法

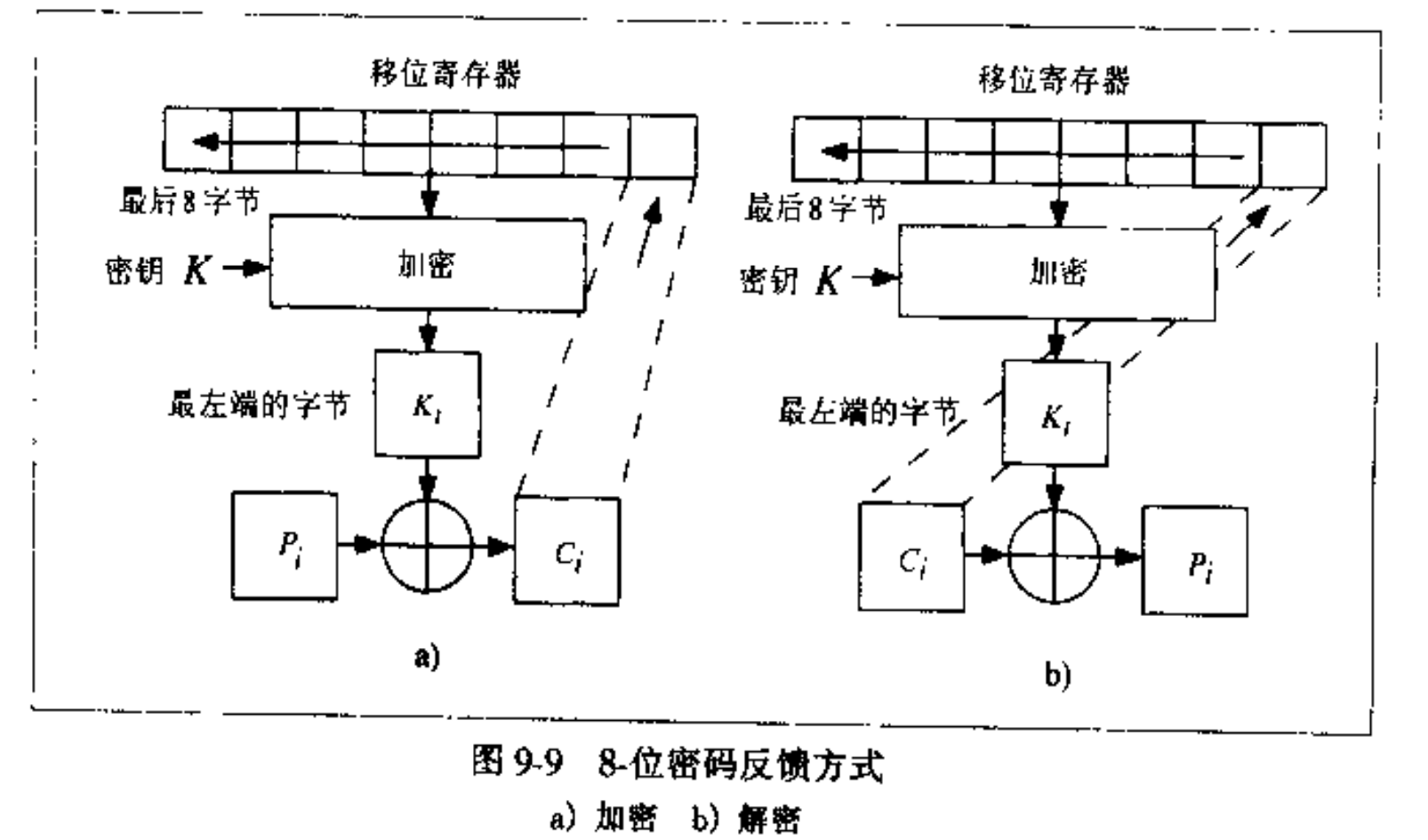
Cipher Feedback Mode（CFB）中文名称是：密文反馈模式。CFB是要在加密过程中，用密文去进行下一步的加密，这类似于CBC的操作，也就有初始向量IV的引入。而与CBC不同的是，在加密时采用的是类似OFB的模式，是对”处理后的IV和加密后密文“进行加密，然后得到的密钥再与明文XOR运算，得到密文，密文用于进一步的加密，以此往复。CFB在加密解密过程中，一次处理的是s比特，而不是AES的块规模128比特。那么，如果s=1，那就是一次加密一个比特。CFB相对难以理解，这里说明一下加密操作流程（解密类似），以s=1，加密方法采取AES为例。

在加密第一个块时，首先对IV进行加密，得到128比特的比特串，然后取出第一个比特与明文第一个比特进行XOR运算，得到第一个密文比特，保存IV剩下127个比特（不是IV加密结果的后127比特）。在第二轮加密第二个比特时，将上一轮127个比特向左移位一位（IV的后127比特），并把第一个比特的密文添加到最后，得到类似于CBC中每一轮密文作用的比特串；对这个比特串加密后，取出第一个比特与明文第二个比特做XOR运算，得到第二个密文比特。之后往复循环，解密亦是同理。为了更好的理解这个移位的操作，截取了[^12]的图。其中，移位寄存器首先存放的是IV，然后每一轮加密左移s位，将上一轮的s位输出密文填充到右侧末尾，用于加密生成密钥流。

根据openssl的文档^13，在Shadowsocks支持的aes-256-cfb中，s=128，与IV的长度一致，是AES标准的加密长度。而cfb1和cfb8分别对应s=1和s=8。

在CFB 模式中，明文的一个错误就会影响所有后面的密文以及在解密过程中的逆。密文出现错误就更有趣了：首先，密文里1位的错误会引起明文的一个单独错误，除此之外，错误进入移位寄存器，导致密文变成无用的信息，直到该错误从移位寄存器的另一端移出。在8位 CFB模式中，密文中1位的错误会使加密的明文产生 9 字节的错误。之后，系统恢复正常，后面的密文也重新正确解密。通常情况下，在n位 CFB 模式中一个密文错误会影响当前和随后的m/n-1个分组的解密，其中 m 是分组大小。（我认为这里的 当前是已经进入寄存器的时刻，与下文不冲突）

该类错误扩散的一个严重问题是，如果Mallory 熟悉某个正在传输的明文，他就可以篡改某个分组里的某些位，使它们解密成自己想要的信息。下一个分组会被解密成“垃圾”，但破坏已经发生了。他还可以更改消息的最后一些位而不被发现。

CFB模式对同步错误来说，同样是自恢复的。错误进入移位寄存器就可以使8字节的数据毁坏，直到它从另一端移出寄存器。CFB 是分组密码算法用于自同步序列密码算法的一个实例 （分组级）。

而针对Shadowsocks的aes-256-cfb，一个错误只会影响当前（被篡改明文）和下一个分组的解密（这组密文进AES加密获得密钥流）。这里需要说一下“下一个分组的解密”，就是引用中的当前分组的解密，随后的是128/128-1=0，共影响这一个解密，不冲突。这里和后面记录的ss漏洞紧密相连，相当于做一个铺垫。

以下是我的个人理解，可能有误。

但是不论s=1/8/128，CFB都可以作为流加密模式。以128位为例说明，首先会生成128比特的被用于与明文XOR的密钥流，这可以用于加密任意小于128位长度的明文；而未使用的密钥流部分，可以在下一次加密时继续使用；当达到128比特密文时，就可以将其作为密文反馈送入移位寄存器，生成接下来128位的密钥流。这些具体记录和实现，就是由openssl的CTX上下文管理的。

在解密时也是如此，到达了多少数据解出多少明文，比如一开始只到达了IV和160比特密文，就用AES加密IV得到的128比特密钥流与密文前128比特进行XOR运算，得到前128比特明文；然后将前128比特密文送入AES，得到129-256比特密钥流，将129-160比特用于和129-160比特密文异或得到完整明文。当又一次从套接字取到100比特数据时，将之前的161-256比特密钥流与第二次的1-96比特密文进行XOR运算，得到第二次的1-96比特明文；然后将第一次的129-160比特密文和第二次的1-96比特密文（共128比特）输入AES得到257-384比特密钥流，用于解密第二次收到的97-100比特。完成数据的随到随解密。

在早期教程，常常选用的aes-256-cfb，就是这样的组合，256位密钥的AES方法，搭配CFB操作模式。当然，这也有着OFB一样的弱点，即比特一一对应，数据流被篡改可能造成被检测的问题。这说明，我们需要增加对报文完整性的验证，在数据被篡改时做出反应，也就出现了另一类方法：GCM。

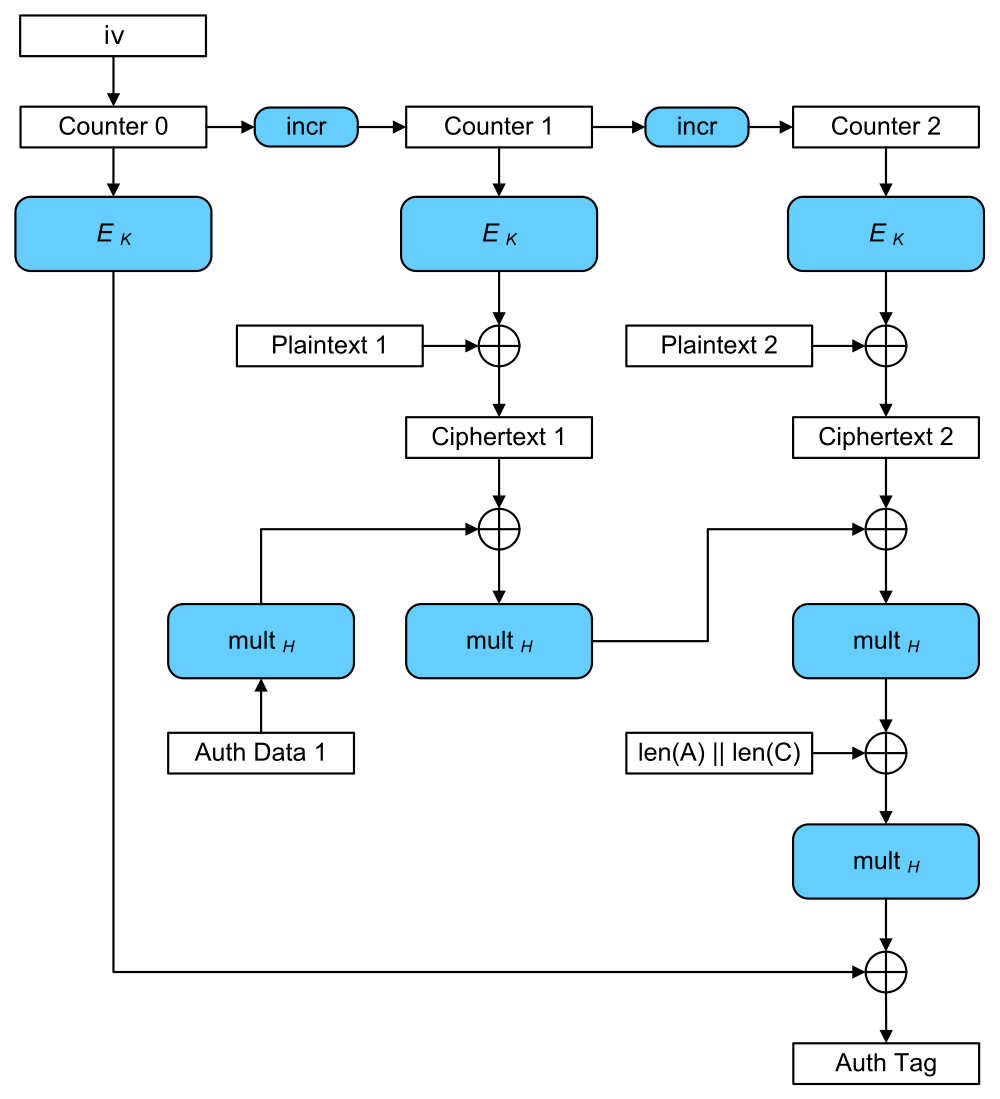
Galois/Counter Mode模式-面对OFB类加密的补丁，增加完整性校核和一定程度的鉴别性

这部分我在这里先简单略过，在回顾到Shadowsocks相关部分时，再以NIST SP 800-38D为基准展开记录一点，而且下文的消息验证码，也是必要的知识。

从图中可以明显看到CTR的影子，并且CTR是由IV生成的；此外还加了一个消息验证码式的Tag标签。别的就在后面再记录了。

公开密钥密码

所谓公开密钥密码，我自己又习惯性叫做非对称加密，以与对称密钥区分。与对称密钥不同的是，非对称加密时加密解密用的是两个密钥：公钥和私钥。在这里记录的是基于RSA（公开密钥密码中的一类）的一些基本概念。这里与原版Shadowsocks毫无关联，是TLS/SSL中的重要组成部分。

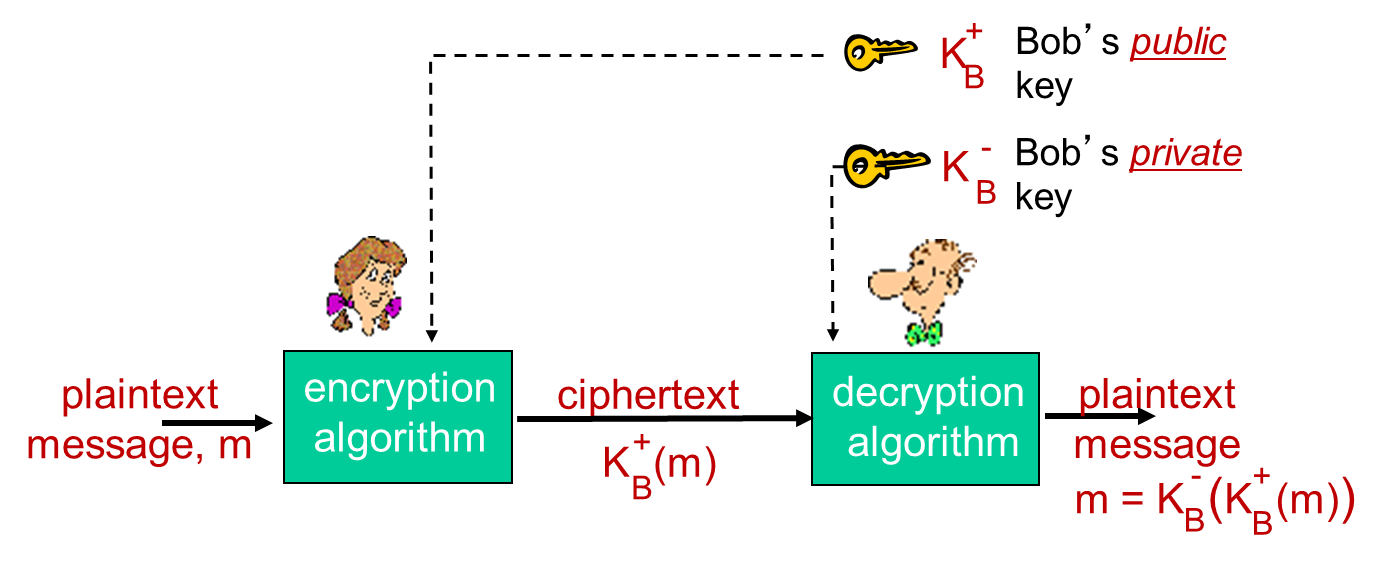
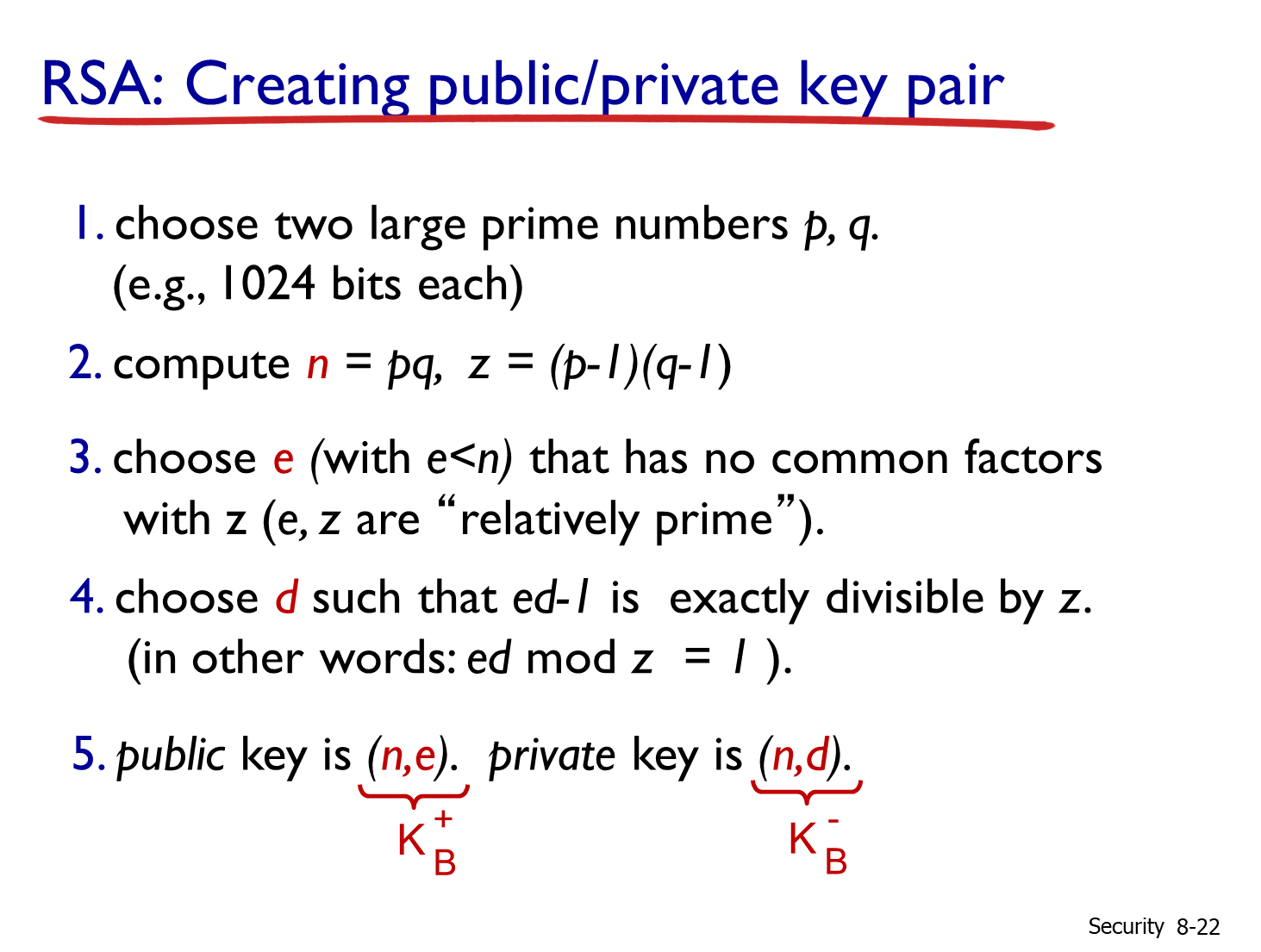
在RSA的密钥对生成过程中，选择了两个大质数：p和q，二者乘积为n=pq，进而基于n，按照一定要求去选择两个数e和d，其中e 通常选择为与 (p-1)(q-1) 互质的数，而 d 是 e 模 (p-1)(q-1) 的模反元素。(n,e)作为公钥，(n,d)作为私钥。具体如下图所示：

需要注意的是，公钥和私钥，本质上就是两个数字，在加密解密过程中，需要用这两个数字对明文密文进行计算。而RSA有一个重要的特性：公钥和私钥在数学上是等价的，也就是说：公钥加密的信息，可以用私钥解密；私钥加密的信息，可以用公钥解密；而公钥/私钥各自加密的消息，是不能通过公钥/私钥自己解密的。具体来说，就要涉及到加密和解密的操作。被加密明文可以通过编码（ASCII、UTF-8）看成一个数字，对于公钥加密私钥解密的场景而言，加密操作是c=m^e mod n，解密操作是m=c^d mod n，其中m是明文，c是密文。这依赖于e、d的选择和一个数学运算m=(m^e mod n)^d mod n。

之所以无法从加密密钥直接逆向运算得到明文，是因为这个mod操作：有m=k*c+n，其中k是正整数。如果要这么解密需要做极多次尝试，并且每次产生尝试完都会得到一串数字，需要判断是否是明文，所以不可行。

而由于公钥加密的信息，可以用私钥解密；私钥加密的信息，可以用公钥解密这个特性，出现了两类应用场景：

• 完整性、身份认证场景：私钥签名----->公钥验签。如CA证书解密，确保是受信任证书颁发结构发出的，未被篡改的证书。
• 保密场景：公钥加密----->私钥解密。如TLS的密钥协商：浏览器生成随机数，通过公钥加密后传给server，之后用于加密，只有二者知道。

基本的概念和应用场景记录完了，下面记录一个现实一些的问题：公钥和私钥在数学上的等价性可以使其在使用过程中互换吗？[^9 ]

答案是否定的，这是因为

1. 在实际的私钥文件中，除了(n,d)对外，还保留了p、q等额外信息，可以用于生成公钥。
2. 虽然算法要求公钥的e是随机选取的，但在实际工程应用，往往将其固定为3或65537，这会暴露公钥私钥错误配置的信息。

因此，一定要保证私钥用于解密和签名，而公钥用于加密和验证签名。

散列函数

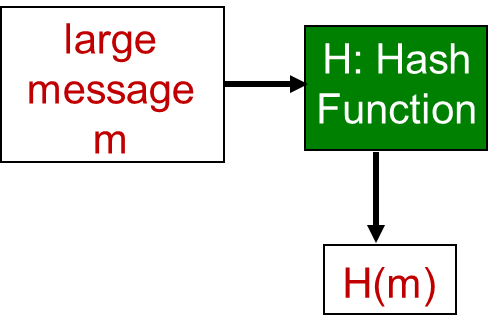
散列函数又称为哈希函数（Hash function），它用于将输入数据（通常是任意长度的消息或密码）转换为固定长度的输出，通常是一个固定大小的二进制串。具有以下特性：

1. 固定长度输出： 密码散列函数的输出是一个固定长度的二进制串，无论输入的消息有多长。
2. 不可逆性： 密码散列函数应该是单向的，即难以从散列值反推出原始输入。这种特性是为了确保密码散列函数不容易被逆向破解。
3. 抗碰撞性： 密码散列函数应该是抗碰撞的，即不同的输入不应产生相同的散列值。这是为了防止两个不同的输入产生相同的散列值，提高密码散列函数的安全性。
4. 散列值随机性： 密码散列函数的输出应看起来是随机的，即使输入只有微小的变化。
5. 效率： 密码散列函数应该是高效的，能够在合理的时间内计算出输出。
6. 密钥不可推导性： 在一些场景中，密码散列函数可能接受一个密钥作为输入，但即使知道密钥和散列值，也难以推导出原始输入。

这些特性使得散列函数，主要用于保证报文完整性，比如对一条数据生成“摘要”，通过对比收到数据生成的散列和公示的散列值，验证数据是否被修改。此外，散列函数也可以与消息验证码结合，提供更强的报文完整性检测及一定的鉴别性。散列函数还可以和数字签名技术相结合，提供更强的安全性保障。总而言之，散列函数的应用是更为灵活的，存在着诸多的可能。

在Shadowsocks2.9.1中，散列函数被多次应用，用于从密钥派生出密钥甚至于初始向量，这利用了散列函数固定长度输出且不可逆的特点，是在encyypt.py的EVP_BytesToKey函数中：

    

#encrypt.py

def EVP_BytesToKey(password, key_len, iv_len): #用密码生成key和iv

#equivalent to OpenSSL's EVP_BytesToKey() with count 1

#so that we make the same key and iv as nodejs version

​    cached_key = '%s-%d-%d' % (password, key_len, iv_len)
​    r = cached_keys.get(cached_key, None)
​    if r:
​        return r
​    m = []
​    i = 0
​    while len(b''.join(m))  0:
​            data = m[i - 1] + password #前一个md5加password 进而进一步生成md5 password用来生成原始数据 类似报文鉴别码？
​        md5.update(data)
​        m.append(md5.digest()) #m 是一个列表，md5.digest() 返回一个包含 MD5 摘要的原始字节串（bytes）。append() 方法将这个字节串添加到列表 m 中
​        i += 1
​    ms = b''.join(m)
​    key = ms[:key_len]
​    iv = ms[key_len:key_len + iv_len] #生成的128bit串联的字节串 前keylen作为key 后面的作为iv初始向量
​    cached_keys[cached_key] = (key, iv)
​    return key, iv

​    
​    

代码逻辑很简单，先检查是否缓存了派生的符合长度的密钥。在没有缓存时，就通过password（也就是配置文件中大家设置的），生成md5摘要，存入列表m；将md5摘要与密钥连接，再次生成md5摘要，存入列表m；以此往复，直到达到符合要求的长度，返回生成的密钥和IV。

但是这种方法，现在已被启用，安全性过于简单，可以撞库。并且在SIP022有如下描述：

Unlike previous editions, Shadowsocks 2022 requires that a cryptographically-secure fixed-length PSK to be directly provided by the user. Implementations MUST NOT use the old EVP_BytesToKey function or any other method to generate keys from passwords.

报文鉴别码

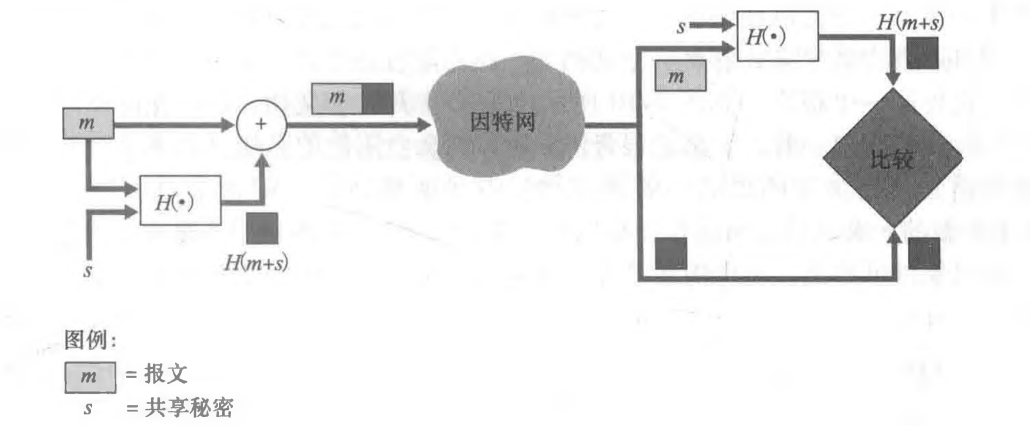
为了执行报文完整性，除了使用密码散列函数外，Alice和Bob将需要共享秘密s。这个共享的秘密只不过是一个比特串，它被称为鉴别密钥(authentication key)。使用这个共享秘密，报文完整性能够执行如下：

1 ) Alice生成报文m,用s级联m以生成m+s,并计算散列H(m+s) (例如使用 SHA-1) 。H(m + s)被称为报文鉴别码(Message Authentication Code, MAC)

2） 然后Alice将MAC附加到报文m上，生成扩展报文（m, H（m+s））,并将该扩展报文发送给Bob。

3） Bob接收到一个扩展报文（m，h）,由于知道s,计算出报文鉴别码H（m+s）。如果H（m+s） =h, Bob得到结论：一切正常。

报文鉴别码（Message Authentication Code，MAC)，本质上是一个处理后的散列函数结果，也就是加了认证的“数据摘要”。展开来说，MAC是与散列函数结合的一种技术，它在散列函数保证报文完整性的基础上，增强了报文完整性，并添加了鉴别性。具体而言，加密解密双方需要共享一个鉴别密钥，在散列函数计算前，将这个鉴别密钥附加到原始报文上，而后再由散列函数得到MAC。

需要说明的是，这里使用的报文，而不是密文，是因为MAC并不是用来保证机密性的手段，它是用来保证完整性和鉴别性的。数据可以明文发送，明文+MAC也是一种应用场景。

在同时通过网络发送报文和数据摘要时，如果入侵者修改了报文，并按照相同的散列函数算法生成了摘要，就会无法检测出完整性遭到损害。而入侵者没有生成MAC的鉴别密钥，就无法生成修改后的MAC，从而实现一定程度的鉴别性。这种方法在GCM加密方法中也有所体现，是用来生成Tag或者GMAC的核心思想。

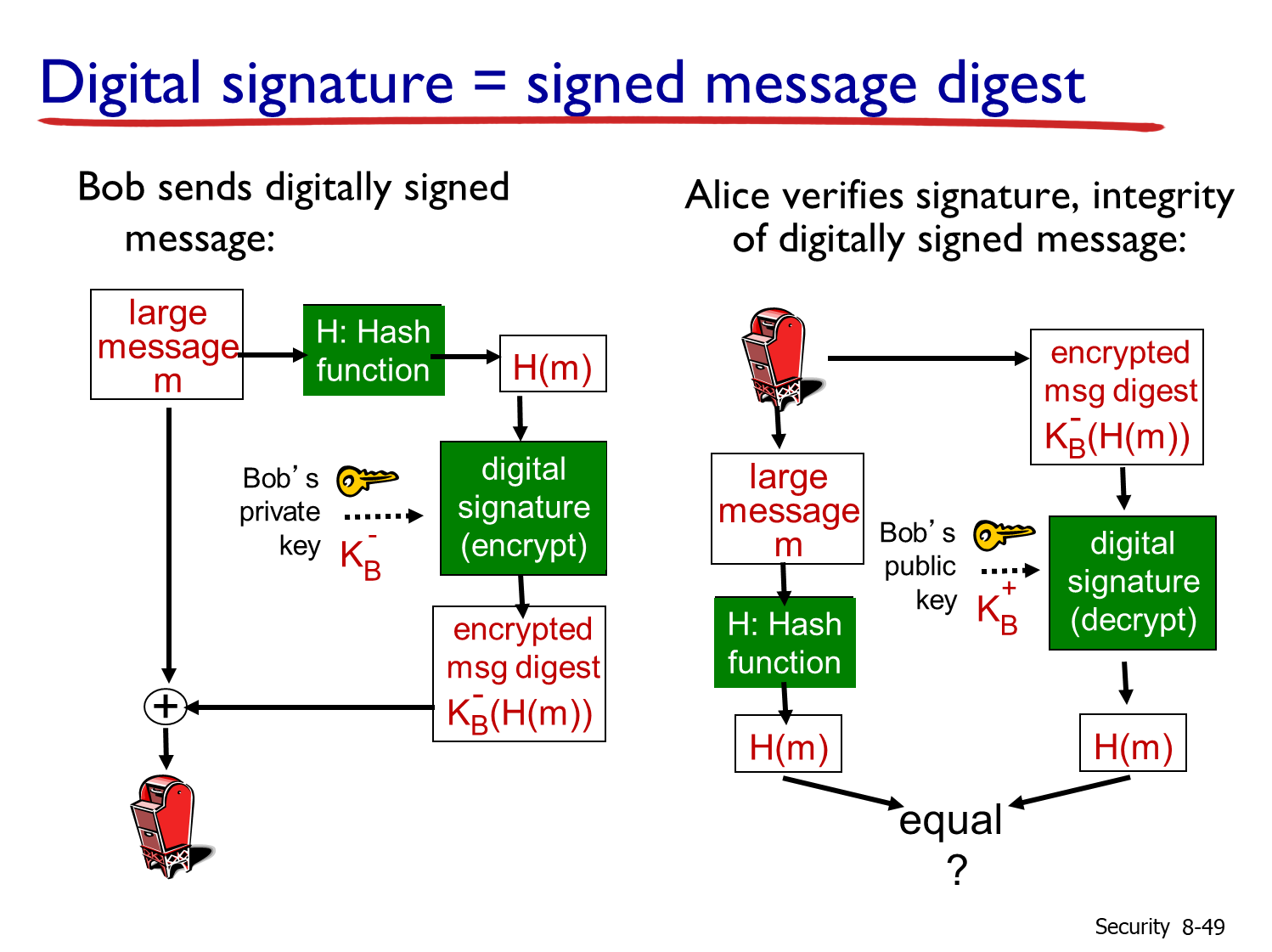
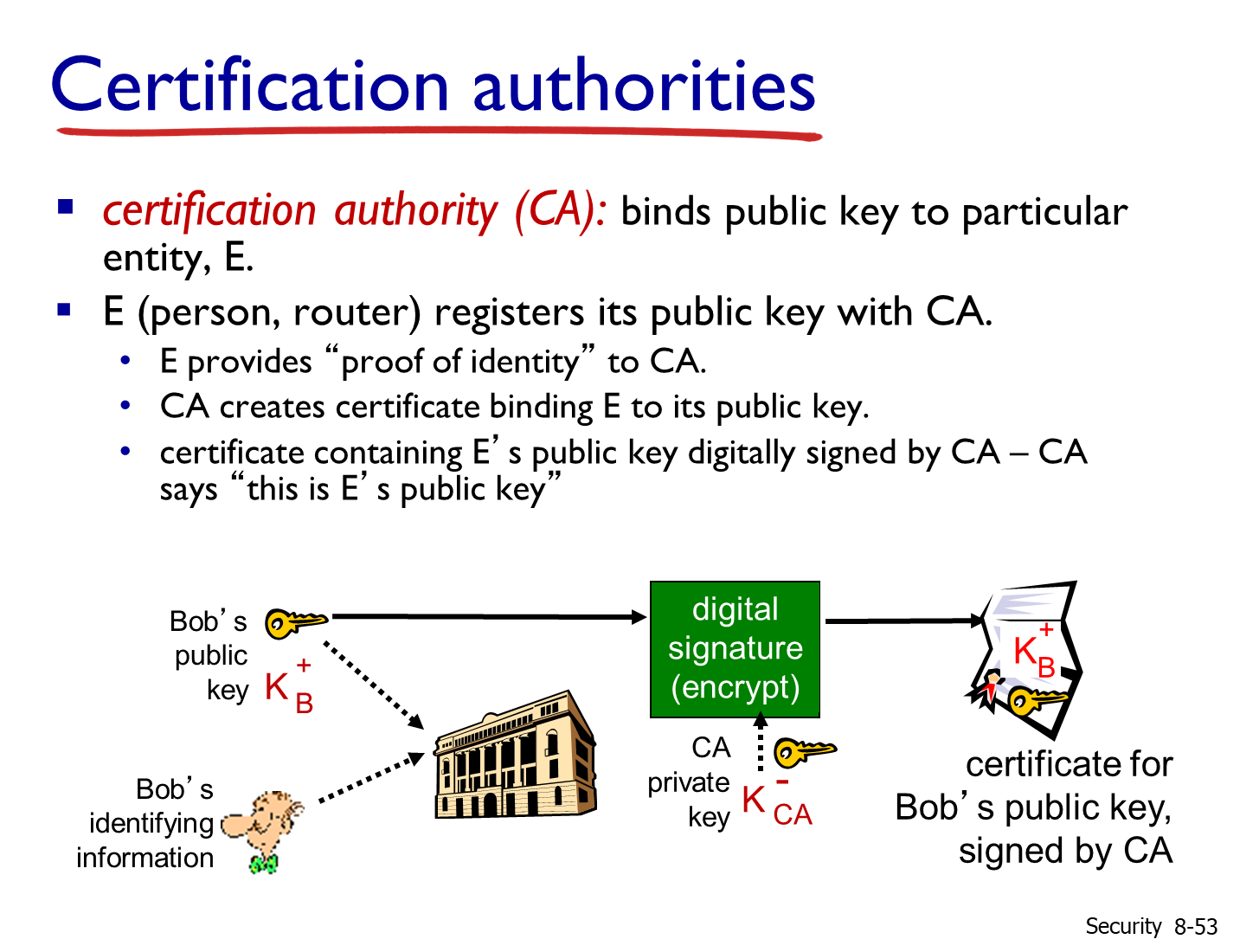
数字签名及公钥认证

数字签名与公钥认证是前文散列函数和公开密钥密码的结合及进阶应用。在对鉴别性和完整性有要求的场合下，因为RSA算法加解密消耗高，远不如对称加密算法，所以一个策略是对报文的摘要进行私钥加密。摘要被私钥加密后难以修改，完整性得以保证；私钥带有身份认证功能，实现鉴别性的要求。也就是在公开密钥密码部分记录的：在完整性、身份认证场景下，可以用私钥签名----->公钥验签。

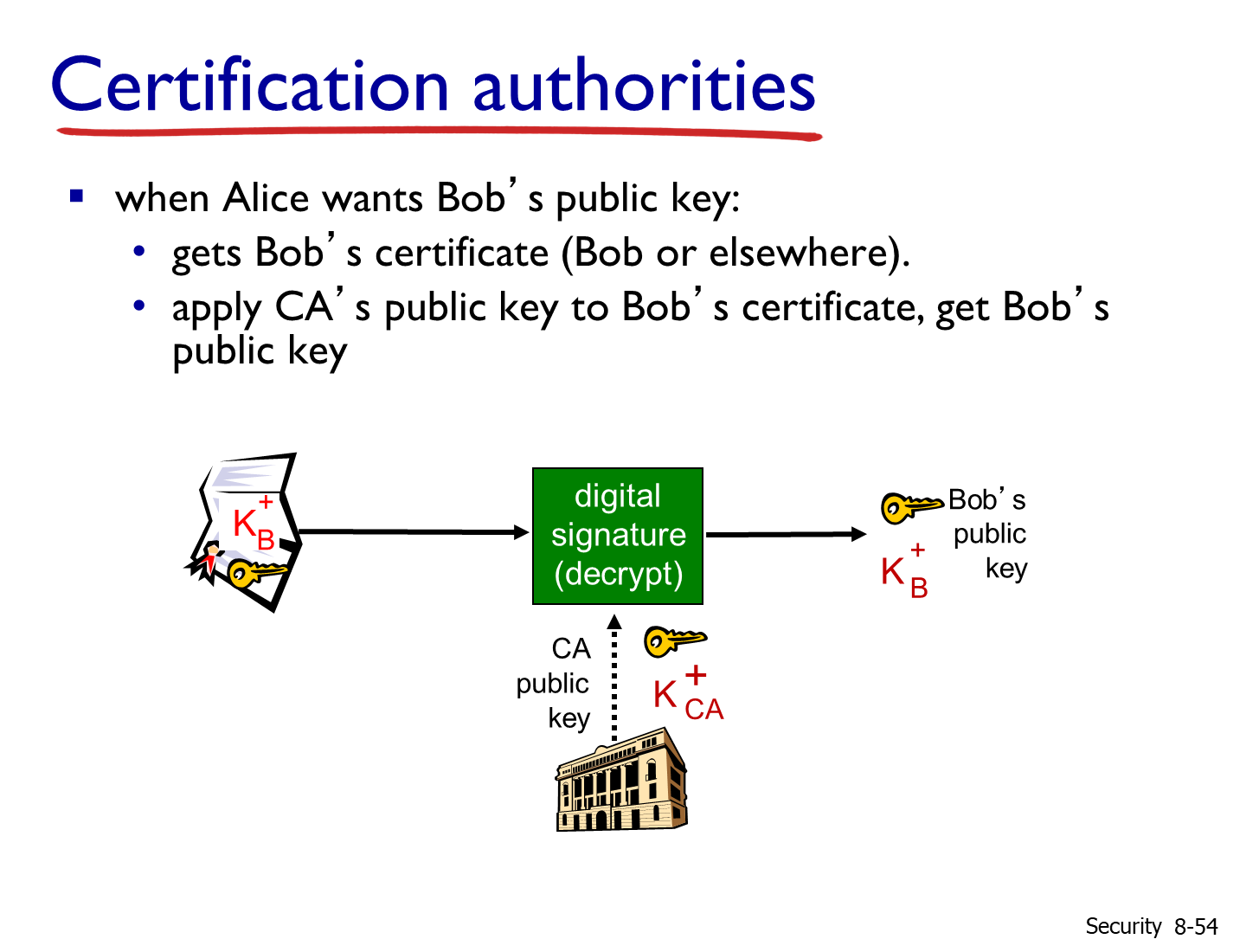
而另一个需要解决的问题是：如何保证拿到的公钥确实是签名方的公钥？如果通讯被中间人拦截，修改了原本是发送方的公钥，变成了中间人的公钥，那么私钥签名的效力也就没有了。而目前的策略就是公钥验签：通过认证中心（Certification Authority，CA）对通信方提供的信息（包含公钥及其他证书信息）的摘要进行签名；在双方通信时，发送方发送自己的证书给接收方（其中证书包括公钥、认证信息，以及CA私钥签名的信息摘要），接收方用CA的公钥进行验签，认证证书确实是来源于CA的，这样就能确保得到是通信方的真实的公钥。而CA的公钥会在设备（例如浏览器）里内置，确保确实是CA的公钥，这样实现了信任链的闭合。

不重数

不重数（nonce）是用来防止重放攻击（replay attack）的一种技术。重放攻击是指攻击者截获并重新发送先前的有效消息，以欺骗系统。通过在通信中引入不重数，每个消息都具有唯一的标识，因此即使攻击者截获了一个消息并尝试重放，由于不重数不同，系统能够识别并拒绝这个重复的消息。

初始向量IV是在对称加密中使用的一个重要工具，确保每次加密相同的明文时产生不同的密文。如果初始向量被重用，可能导致加密的泄露，因为相同的明文会产生相同的密文，使得攻击者更容易识别模式。在生成IV时，也最好有与不重数一样的方法和注意事项。

不重数在TLS中也扮演着重要作用，在生成会话密钥时，确保这个协商的安全性。

Shadowsocks的加密需求

在下文的记录中，Shadowsocks应用于一个特殊场景：在校园网内上网。我们有时可能会在厕所的墙上看到一些不太健康的网站，访问去看一些不健康的小视频，而我们学校的防火墙会检测这些网站，如果被发现了还会被辅导员找谈话。即便有着TLS对HTTP交互内容进行加密，但是SNI还是会暴露我们的访问意图。所以，我们想找到一种代理方式，让SNI都对校园网管理员不可见，经过诸多寻找，我们找到了这个能实现该功能的程序：Shadowsocks。后文的部分内容，均聚焦于如何和校园网管理员玩捉迷藏。

Shadowsocks，这个名字就已经说明了它的主要功能：shadow+socks。按我的个人理解，其中socks特指是socks5协议，shadow意指遮蔽，shadowsocks就是将socks5的特征遮蔽起来，从而实现跨越校园网防火墙检测的访问。

在早期，即2.9.1的shadowsocks中，最重要的是机密性，而不是鉴别性和完整性。故早期采用的都是对称加密的流加密方法。（一个例子就是aes-256-cfb，我在七八年前时候第一次搭建的时候就用的这个方式，现在终于明白是什么了，感叹）。Clowwindy有过如下的发言[^10]（引用部分已针对本文学习场景修改）：

SSL 设计目标:

1. 防内容篡改
2. 防冒充服务器身份
3. 加密通信内容

而绕过学校防火墙的目标:

1. 不被检测出客户端在访问什么网站
2. 不被检测出服务器在提供能看小黄网服务

SSL 和这个目标还是有一些出入。其中最大的问题是，2. 防冒充服务器身份 这个功能多余了。他会导致学校防火墙嗅探出证书信息，继而学校防火墙会知道服务器身份。如果学校防火墙知道一个服务器身份是用来看小黄网站的，它要做的仅仅是封掉使用这个证书的所有 IP。

学校防火墙看见的 SSL 握手响应头部如下：

.......

这也说明了为什么Shadowsocks没有选取高机密性的RSA相关方法。在不考虑DPI（深度包检测）时，我们需要的只是无法被看出意图的数据流，不要像HTTP有HTTP Header，socks5有明确的握手数据包等。那么加密就是一个很好的方案，加密后的数据类似于乱码，有着很大的随机性，在黑名单形式下的学校防火墙不能断定我们在看小视频，就不会直接把我们的server拉黑。所以在早期版本的Shadowsocks中，对加密的强度要求很低，以混淆数据流为目的。

本质上来说：Shadowsocks是一个代理程序，但是在互联网暴露的数据流中进行了加密混淆处理，也就是数据传输时套了一个加解密函数的调用。所以之前花了大篇幅记录TCP的代理是如何实现的，作为一个力学系学生，头一次接触，收获颇多，感觉什么值得记下来就记下来，结果记了一大堆......

此外，Clowwindy有一个调侃的评论值得记录下来：

因为 chacha20 从 x86 上的性能来看，对速度的影响太小，提高还太有限，不如换个思路，因为通信包到了终端以后，走的都是电路，这里其实涉及到一个供电体系的问题，更换加密不如换一个电网，同一个 VPS，同一个路由器，但是，改用核电给路由器供电时，比火电丢包率会降低一个数量级，大大提高 TCP 吞吐率，经测试这是目前速度最快的供电方式，甚至优于水电，同理选 VPS 机房也要看供电，有些号称用了绿色能源，其实效果不好，这里面其实还涉及到选用 UPS 的型号，就不细说了 另外说到硬件加速，连接路由器的网线也很重要，建议用六类屏蔽线，不过一定不能买那种超薄扁平的网线，会对带宽起到整形作用，突发上不去，看 4K 会受影响，数据可能不准，不过大概也体现了差异 今天没有时间再次测试了，就发这么多吧。你们有一个好，出个新功能，写教程比别人都快，但试来试去的结论，太简单，有时太朴素了，我感觉你们还需要学习，提高自己的知识水平，将来如果写的教程有偏差，你们要负责

还有rlei的评论：

讨论shadowsocks不同加密方式的安全性没有意义。shadowsocks是被设计来混淆数据，增加某Wall检查出流量特征所需的计算量，提高实时检测的成本，而不是加密。ss的作者多次强调过这一点

这二者均来源于[^11]，感谢网友的留档。

而后简单的流加密被发现有漏洞，密文被学校偷偷修改后，会造成服务器被学校检测出来[^5]，在流密码的基础上就出现了两种变化：一来换成块加密方法，这涉及数据块的填充和操作；二来是给加密方法增加完整性校核，这样就使用AEAD类的加密方法，包括且不限于GCM方法。而目前的Shadowsocks的实现应该是聚焦于后一类方法，我也是深受aes-256-gcm的名字影响，去阅读了NIST SP 800-38D。这样数据如果被修改，解密时就会由于一个类似MAC的Tag验证失败，而导致解密失败。之后服务器就可以执行一系列异常处理操作，以规避检测。这些在Shadowsocks2.9.1的代码中没有体现，接下来的代码分析并不包含这部分，只是记录最初流加密的方式。

Shadowsocks2.9.1 在代码层次是如何实现加密的？

这里以我曾经最爱用的aes-256-cfb为例说明，由前面的铺垫可知，采用了256位密钥的AES方法；而AES的CFB操作模式中，每次加密的比特数是AES固定的128比特，所以初始向量也是128比特大小。这是存储在openssl.py的ciphers列表字典中，记录了支持的加密方法，以及其对应的密钥（key）长度和初始向量（IV）长度，以及创建该加密的对象的类（有的加密方法第三个参数是创建加密的对象的函数）。

    

​    

#openssl.py
ciphers = {
    'aes-128-cfb': (16, 16, OpenSSLCrypto),
    'aes-192-cfb': (24, 16, OpenSSLCrypto),
    'aes-256-cfb': (32, 16, OpenSSLCrypto),
    'aes-128-ofb': (16, 16, OpenSSLCrypto),
    'aes-192-ofb': (24, 16, OpenSSLCrypto),
    'aes-256-ofb': (32, 16, OpenSSLCrypto),
    'aes-128-ctr': (16, 16, OpenSSLCrypto),
    'aes-192-ctr': (24, 16, OpenSSLCrypto),
    'aes-256-ctr': (32, 16, OpenSSLCrypto),
    'aes-128-cfb8': (16, 16, OpenSSLCrypto),
    'aes-192-cfb8': (24, 16, OpenSSLCrypto),
    'aes-256-cfb8': (32, 16, OpenSSLCrypto),
    'aes-128-cfb1': (16, 16, OpenSSLCrypto),
    'aes-192-cfb1': (24, 16, OpenSSLCrypto),
    'aes-256-cfb1': (32, 16, OpenSSLCrypto),
    'bf-cfb': (16, 8, OpenSSLCrypto),
    'camellia-128-cfb': (16, 16, OpenSSLCrypto),
    'camellia-192-cfb': (24, 16, OpenSSLCrypto),
    'camellia-256-cfb': (32, 16, OpenSSLCrypto),
    'cast5-cfb': (16, 8, OpenSSLCrypto),
    'des-cfb': (8, 8, OpenSSLCrypto),
    'idea-cfb': (16, 8, OpenSSLCrypto),
    'rc2-cfb': (16, 8, OpenSSLCrypto),
    'rc4': (16, 0, OpenSSLCrypto),
    'seed-cfb': (16, 16, OpenSSLCrypto),
}
    

加下来我们就来一次自下向顶的记录，去学习OpenSSLCrypto类的实现。不过在这之前，需要明确openssl的上下文（context，CTX）的概念，这是对数据流连续不断加密的核心部件。下面取chatgpt的描述：

具体来说，在 OpenSSL 中，上下文（ctx）通常是一个结构体或对象，它包含了与某个特定任务相关的各种信息。这些信息可能包括：

1. 状态信息： 表示任务的当前状态，例如加密或解密的进展情况。
2. 配置参数： 包括算法、密钥、模式等配置，以确保任务按照期望的方式执行。
3. 环境信息： 与任务执行环境相关的信息，例如随机数生成器的状态。

通过将这些信息存储在上下文中，可以在多次调用之间保持一致的状态，从而使得连续的操作能够协同工作，并且更容易进行定制和配置。这种设计模式提高了代码的可维护性和可扩展性，同时也使得代码更易于理解和调试。

当你在使用 OpenSSL 进行加密操作时，你通常会执行以下步骤：

1. 创建上下文（Context）： 使用 OpenSSL 提供的函数创建一个上下文对象（CTX），并配置相应的参数，如选择加密算法、设置密钥等。
2. 初始化上下文： 对上下文进行初始化，确保它处于一个合适的起始状态。
3. 连续加密/解密操作： 使用初始化过的上下文对象进行多次的加密或解密操作，处理数据流的不同部分。
4. 清理上下文： 在完成所有加密或解密操作后，进行清理和释放资源，确保安全关闭。

而openssl提供的接口有如下功能：

在使用 OpenSSL 的 EVP 接口时，你通常会使用一系列函数来创建、配置、使用和销毁密码算法上下文。这包括：

1. EVP_CIPHER_CTX_new(): 创建一个新的密码算法上下文。
2. EVP_CipherInit_ex(): 初始化密码算法上下文，配置算法、密钥和其他参数。
3. EVP_CipherUpdate(): 加密或解密数据。
4. EVP_CipherFinal_ex(): 完成加密或解密操作。
5. EVP_CIPHER_CTX_free(): 释放密码算法上下文。

回到Shadowsocks2.9.1的源码中，有关类的函数是如下实现的：

    

​    

#openssl.py
class OpenSSLCrypto(object):
    def __init__(self, cipher_name, key, iv, op): #op==1是用于加密 =0解密
        self._ctx = None
        if not loaded:
            load_openssl() #加载模块
        cipher_name = common.to_bytes(cipher_name)
        cipher = libcrypto.EVP_get_cipherbyname(cipher_name) #返回输入加密方式的 密码的上下文信息
        if not cipher:
            cipher = load_cipher(cipher_name)
        if not cipher:
            raise Exception('cipher %s not found in libcrypto' % cipher_name)#加密不可用 则抛出有提示的异常
        key_ptr = c_char_p(key)
        iv_ptr = c_char_p(iv) #是 ctypes 中用来处理 C 字符串指针的类型。在这个上下文中，key_ptr 和 iv_ptr 是 C 字符串指针，指向密钥和初始化向量。
        self._ctx = libcrypto.EVP_CIPHER_CTX_new()  #加密算法上下文是一个数据结构，它包含了在加密和解密操作中所需的参数和状态信息。在 OpenSSL 中，使用 EVP_CIPHER_CTX_new() 创建一个加密算法上下文，该上下文存储了算法的密钥、初始化向量以及其他必要的信息，供加密和解密函数使用。
        #初始向量还没有被使用，这个操作主要是为了准备进行加密和解密操作所需的上下文环境。初始向量将在实际的加密过程中使用，但在这个特定的步骤中暂时与创建上下文无关。
        if not self._ctx:
            raise Exception('can not create cipher context')
        r = libcrypto.EVP_CipherInit_ex(self._ctx, cipher, None,
                                        key_ptr, iv_ptr, c_int(op)) #该函数会将上下文 _ctx 初始化为执行加密操作所需的状态。传递 None 到第三个参数表示不使用特定的加密模式，而是使用默认的模式。 反之是解密状态？
        if not r:
            self.clean()
            raise Exception('can not initialize cipher context')
        #EVP_CIPHER_CTX_free 将释放整个上下文对象，包括内存和其他资源，而 EVP_CIPHER_CTX_cleanup 则只是清理该上下文的内部状态，不会释放实际的内存空间。
        #先clean再free

    def update(self, data):#返回数据的加密值
        global buf_size, buf
        cipher_out_len = c_long(0) #ctype对象
        l = len(data)
        if buf_size 

可见前面列出的EVP的4个接口在这里被调用，其中创建上下文和初始化上下文，是在类的构造函数完成的；加密解密是在Update方法实现的；释放密码上下文，是在删除时实现的。

在构造函数中，需要传入加密方法，密钥key和初始向量（由配置文件password通过EVP_BytesToKey生成），以及是加密或解密的参数（op）。其中密码上下文通过libcrypto.EVP_CIPHER_CTX_new() 生成，加密方法的密码上下文通过cipher = libcrypto.EVP_get_cipherbyname(cipher_name)生成，二者均作为参数传入初始化上下文r = libcrypto.EVP_CipherInit_ex(self._ctx, cipher, None,key_ptr, iv_ptr, c_int(op))完成整体加密对象的初始化。

在update方法中，传入要加密/解密的数据，调用EVP_CipherUpdate方法完成加密/解密，并将完成加密/解密后的数据返回，实现了对Openssl的封装。这样，只要调用OpenSSLCrypto().update(待处理数据)，即可完成加密解密的操作。

值得记录的是，在创建加密方法的密码上下文时，会优先使用libcrypto.EVP_get_cipherbyname方法，但是在无法直接找到时，会尝试用直接通过load_cipher函数去找该加密方法密码上下文的结构体，如果还失败，则进入异常处理。函数如下，其中return cipher()的()是完成结构体的初始化：

    

def load_cipher(cipher_name):  #返回输入加密方式的 密码的上下文结构体
    func_name = 'EVP_' + cipher_name.replace('-', '_')
    if bytes != str:
        func_name = str(func_name, 'utf-8')
    cipher = getattr(libcrypto, func_name, None)
    if cipher:
        cipher.restype = c_void_p
        return cipher()#（）是结构体的初始化
    return None

    

比较详细的记录都在函数注释里，有了这些基础知识，代码应该就很好看了。

至于加密库的导入，是通过load_openssl函数实现的。

    

    #openssl.py

def load_openssl():
    #只要从crypto或eay32中找到EVP_get_cipherbyname有这个方法的文件就行 并设定要用的函数输入输出参数 给loaded标记true
    global loaded, libcrypto, buf, ctx_cleanup

    libcrypto = util.find_library(('crypto', 'eay32'),
                                  'EVP_get_cipherbyname',#只要找到EVP_get_cipherbyname有这个方法的文件就行 
                                  'libcrypto')# OpenSSL 的 C 语言库  最后一个只是一个可读名字 不涉及搜寻 return lib = CDLL(path) 返回一个 CDLL 对象，该对象具有加载的动态链接库中的函数的调用接口。
    if libcrypto is None:
        raise Exception('libcrypto(OpenSSL) not found')

    libcrypto.EVP_get_cipherbyname.restype = c_void_p  #c_void_p 是 ctypes 中的一个特殊类型，代表 C 语言中的 void * 类型，用于表示一个不确定类型的指针。在 ctypes 中，它用于处理不同类型的指针对象。
    libcrypto.EVP_CIPHER_CTX_new.restype = c_void_p # Envelope 加密  ///restype用于指定返回的函数结果类型  void是动态类型指针 res是result 结果的缩写 指定结果的返回类型

    libcrypto.EVP_CipherInit_ex.argtypes = (c_void_p, c_void_p, c_char_p,
                                            c_char_p, c_char_p, c_int)

    libcrypto.EVP_CipherUpdate.argtypes = (c_void_p, c_void_p, c_void_p,
                                           c_char_p, c_int)#指定函数参数的类型

    try:
        libcrypto.EVP_CIPHER_CTX_cleanup.argtypes = (c_void_p,)
        ctx_cleanup = libcrypto.EVP_CIPHER_CTX_cleanup
    except AttributeError:
        libcrypto.EVP_CIPHER_CTX_reset.argtypes = (c_void_p,)
        ctx_cleanup = libcrypto.EVP_CIPHER_CTX_reset
    libcrypto.EVP_CIPHER_CTX_free.argtypes = (c_void_p,) #在使用完毕后，清理加密算法上下文以释放资源
    if hasattr(libcrypto, 'OpenSSL_add_all_ciphers'):
        libcrypto.OpenSSL_add_all_ciphers()#这个函数是 OpenSSL 库中的一个函数，用于添加所有的加密算法到内部表中。

    buf = create_string_buffer(buf_size)#是 ctypes 库中的一个函数，用于创建一个指定大小的字符串缓冲区。 此时是2048
    loaded = True

    

其中先寻找包含EVP_get_cipherbyname函数的crypto或eay32(旧名称)库，将其命名为libcrypto。而后由于是使用 ctypes 调用 C 函数，需要restype和argtypes指定返回结果类型的属性和函数参数类型的属性，对EVP接口相关的属性进行设置。最后创建缓存区，并将加载标志置为True。

而util.find_library的实现如下：

    
    #util.py
def find_library(possible_lib_names, search_symbol, library_name):
    import ctypes.util
    from ctypes import CDLL

    paths = []

    if type(possible_lib_names) not in (list, tuple):
        possible_lib_names = [possible_lib_names]

    lib_names = []
    for lib_name in possible_lib_names:
        lib_names.append(lib_name)
        lib_names.append('lib' + lib_name)

    for name in lib_names:
        if os.name == "nt":
            paths.extend(find_library_nt(name))
        else:
            path = ctypes.util.find_library(name)
            if path:
                paths.append(path)

    if not paths:
        # We may get here when find_library fails because, for example,
        # the user does not have sufficient privileges to access those
        # tools underlying find_library on linux.
        import glob

        for name in lib_names:
            patterns = [
                '/usr/local/lib*/lib%s.*' % name,
                '/usr/lib*/lib%s.*' % name,
                'lib%s.*' % name,
                '%s.dll' % name]

            for pat in patterns:
                files = glob.glob(pat)
                if files:
                    paths.extend(files)
    for path in paths:
        try:
            lib = CDLL(path)
            if hasattr(lib, search_symbol):
                logging.info('loading %s from %s', library_name, path)
                return lib #OpenSSL 的 C 语言库
            else:
                logging.warn('can\'t find symbol %s in %s', search_symbol,
                             path)
        except Exception:
            pass
    return None

    

这里主要是处理可能库名，通过ctypes.util.find_library寻找对应路径，最终返回一个CDLL 对象，该对象具有加载的动态链接库中的函数的调用接口，这样就可以用CDLL(dll_path).my_function()完成库函数的调用，与openssl.py中的libcrypto.EVP_get_cipherbyname的用法衔接起来，达成一致。

而OpenSSLCrypto的构造函数需要(self, cipher_name, key, iv, op)作为参数传入，Shadowsocks对此进行了更进一步的封装，做到只需要password和加密方法就能完成加密对象的初始化。

    

    #encrypt.py

class Encryptor(object): #cipher.update封装到Encryptor.encrypt
    def __init__(self, password, method):
        self.password = password
        self.key = None
        self.method = method
        self.iv_sent = False #初始向量
        self.cipher_iv = b''
        self.decipher = None
        self.decipher_iv = None
        method = method.lower()
        self._method_info = self.get_method_info(method) # 'rc4-md5': (16, 16, create_cipher) 返回的是后面的元组
        if self._method_info:
            #是一个对象 OpenSSLCrypto对象 在openssl.py中
            self.cipher = self.get_cipher(password, method, 1,
                                          random_string(self._method_info[1])) #元组的第一个元素 此时op给定1 第四个 初始向量 随机字符串
        else:
            logging.error('method %s not supported' % method)
            sys.exit(1)

    def get_method_info(self, method):
        method = method.lower()
        m = method_supported.get(method)
        return m

    def iv_len(self):
        return len(self.cipher_iv)

    def get_cipher(self, password, method, op, iv): #生成初始向量 最后返回OpenSSlCrypto对象 返回值的update即可加密 封装到Encryptor.cipher 对类Encryptor而言，Encryptor.encrypt就是调用OpenSSlCrypto.update加密  关键是key和iv的生成 相较于OpenSSlCrypto不同
        password = common.to_bytes(password)
        m = self._method_info
        if m[0] > 0:
            key, iv_ = EVP_BytesToKey(password, m[0], m[1]) #keylength是m[0] 用的随机
        else:
            # key_length == 0 indicates we should use the key directly
            key, iv = password, b''
        self.key = key
        iv = iv[:m[1]]#取iv length的长度 这里是输入的随机字符串
        if op == 1:
            # this iv is for cipher not decipher
            self.cipher_iv = iv[:m[1]]
        return m[2](method, key, iv, op)
    #class OpenSSLCrypto(object):
    #def __init__(self, cipher_name, key, iv, op): 加密解密的初始向量 返回了一个OpenSSLCrypto对象 在openssl.py中

    def encrypt(self, buf):
        if len(buf) == 0:
            return buf
        if self.iv_sent: # self.cipher_iv = iv[:m[1]] 其中 key, iv_ = EVP_BytesToKey(password, m[0], m[1]) #keylength是m[0]
            return self.cipher.update(buf)
        else:
            self.iv_sent = True
            return self.cipher_iv + self.cipher.update(buf) #有别于OpenSSLCrypto的加密方式的处理

    def decrypt(self, buf):#没有get——decipher，也就没有 key, iv_ = EVP_BytesToKey(password, m[0], m[1]) 获取iv的过程，直接靠传入的字符串的前面来获得初始向量，实际上通过password计算也能得到？选择方式的问题
        if len(buf) == 0:
            return buf
        if self.decipher is None:#初始化
            decipher_iv_len = self._method_info[1] #元组的第二个元组
            decipher_iv = buf[:decipher_iv_len] #取出初始向量
            self.decipher_iv = decipher_iv
            self.decipher = self.get_cipher(self.password, self.method, 0,
                                            iv=decipher_iv)
            buf = buf[decipher_iv_len:]
            if len(buf) == 0:
                return buf
        return self.decipher.update(buf)
    

Encryptor完成了对负责加密对象的进一步封装：

• 通过password和method生成加密的密钥（key）和初始向量（IV），是之前分析过的EVP_BytesToKey函数实现的。
• 完成了底层加密类的封装，self.cipher = self.get_cipher(password, method, 1,random_string(self._method_info[1]))，将Encryptor的cipher 属性用OpenSSLCrypto(self, cipher_name, key, iv, op)实例赋值，这样就能通过self.cipher.update方法完成加密或解密。
• 完成了对IV在加密解密的处理（当加密明文时，会在第一次返回的密文前加上iv；在解密时，会在第一次解密的密文前提取出iv用于解密），这是encrypt和decrypt函数实现的。

这里最好还是看源代码比较好，文字叙述琐碎而不得全貌，看代码会一目了然。

值得一提的是，在get_cipher方法中，return m[2](method, key, iv, op)初读可能难以理解，按序整理后：

    

    #encrypt.py

class Encryptor(object): 
    m = self._method_info

    self._method_info = self.get_method_info(method)

    def get_method_info(self, method):
        method = method.lower()
        m = method_supported.get(method)
        return m

method_supported = {}
method_supported.update(rc4_md5.ciphers)
method_supported.update(openssl.ciphers)
method_supported.update(sodium.ciphers)
method_supported.update(table.ciphers)

openssl.ciphers = {
    'aes-128-cfb': (16, 16, OpenSSLCrypto),
    'aes-192-cfb': (24, 16, OpenSSLCrypto),
    'aes-256-cfb': (32, 16, OpenSSLCrypto),
    'aes-128-ofb': (16, 16, OpenSSLCrypto),
    'aes-192-ofb': (24, 16, OpenSSLCrypto),
    'aes-256-ofb': (32, 16, OpenSSLCrypto),
    'aes-128-ctr': (16, 16, OpenSSLCrypto),
    'aes-192-ctr': (24, 16, OpenSSLCrypto),
    'aes-256-ctr': (32, 16, OpenSSLCrypto),
    'aes-128-cfb8': (16, 16, OpenSSLCrypto),
    'aes-192-cfb8': (24, 16, OpenSSLCrypto),
    'aes-256-cfb8': (32, 16, OpenSSLCrypto),
    'aes-128-cfb1': (16, 16, OpenSSLCrypto),
    'aes-192-cfb1': (24, 16, OpenSSLCrypto),
    'aes-256-cfb1': (32, 16, OpenSSLCrypto),
    'bf-cfb': (16, 8, OpenSSLCrypto),
    'camellia-128-cfb': (16, 16, OpenSSLCrypto),
    'camellia-192-cfb': (24, 16, OpenSSLCrypto),
    'camellia-256-cfb': (32, 16, OpenSSLCrypto),
    'cast5-cfb': (16, 8, OpenSSLCrypto),
    'des-cfb': (8, 8, OpenSSLCrypto),
    'idea-cfb': (16, 8, OpenSSLCrypto),
    'rc2-cfb': (16, 8, OpenSSLCrypto),
    'rc4': (16, 0, OpenSSLCrypto),
    'seed-cfb': (16, 16, OpenSSLCrypto),
}

rc4_md5.ciphers = {
    'rc4-md5': (16, 16, create_cipher),
}

sodium.ciphers = {
    'salsa20': (32, 8, SodiumCrypto),
    'chacha20': (32, 8, SodiumCrypto),
    'chacha20-ietf': (32, 12, SodiumCrypto),
}

table.ciphers = {
    'table': (0, 0, TableCipher)
}

    

​    

按序一层一层整理后，发现m实际上就是一个包含三个元素的元组：(key_length，iv_length，build_cipher_object_method)，也就是密钥长度，初始向量长度，和加密的实例的构造方法。针对openssl类的，就是直接调用OpenSSLCrypto(cipher_name, key, iv, op)类的构造函数，其包含aes-256-cfb；针对rc4-md5类的就，就是调用create_cipher(alg, key, iv, op, key_as_bytes=0, d=None, salt=None,i=1, padding=1)，返回的也是openssl.OpenSSLCrypto(b'rc4', rc4_key, b'', op)实例，但是是通过函数作为接口。

总而言之，Shadowsocks2.9.1是对Openssl进行了封装，最终通过Encryptor的实例完成加密解密操作，而其中最有用的就是Encryptor的构造函数、encrypt函数和decrypt函数。

针对加密解密，Shadowsocks2.9.1还有测试加密解密速度的函数，有兴趣的话大家可以去看一下，在aes-256-cfb时，确实是可以做到随到随加密，随到随解密。程序生成一个很长的明文，随机打断并加密；而后将整体密文随机打断并解密，判断解密后的明文是否与原始明文相等（assert断言）。这可以说明加密解密的连续性和灵活性。

关于Shadowsocks2.9.1，如何实现加密的，我最后想记录下来的，是Stream ciphers | Shadowsocks后的格式。

Stream_encrypt(key, IV, message) => ciphertext
Stream_decrypt(key, IV, ciphertext) => message

#TCP/UDP的数据流
[IV][encrypted payload]

我主要学习的是TCP的数据流，可见数据流发送时，会先发送IV，而后跟着TCP代理分析中的各自载荷，进行握手或转发。这在最前方的IV，程序中是通过Encryptor类的encrypt(buf)方法的return self.cipher_iv + self.cipher.update(buf)语句是实现的，很值得思考和借鉴。

Shadowsocks向AEAD加密的转变

这一部分一开始没准备学习并记录的，但那样显得又有点不解风情，过于古板了。在阅读了一些材料之后，很有感触，故记录下来。

Shadowsocks容易遭受的已知明文攻击

首先需要说明的是，之前的可以用作流加密的操作模式（CTR,OFB,CFB）实现流加密的方法，均是通过底层加密方法（如AES）按一定方式得到密钥流（可能直接生成极长的密钥流，如CTR和OFB；也可能每加密128位再生成接下来128位的密钥流，如CFB），将密钥流与明文进行XOR运算得到密文。这就导致明文和密文是一一对应的，即明文的第1比特对应于密文的第1比特，明文的第2比特对应于密文的第2比特.....这样就会一定程度上，在加密效果上弱于直接的AES块加密方法：一个比特的错误密文不会扩散到一定长度的解密失败。并且容易受到已知明文攻击：攻击者能够获得一些明文（plaintext）和相应的加密文本（ciphertext）对，在已知明文攻击中，攻击者利用已知的明文和对应的密文之间的关系，以尝试破解加密系统。这种攻击形式对于弱加密算法特别有效，因为在弱算法中，相同的明文可能会被加密为相同的密文，从而暴露出系统的模式和密钥信息。

具体来说：在CTR,OFB,CFB中，都是通过明文 XOR 密钥流得到密文，而如果有一些会出现固定位置的已知明文密文对，如Shadowsocks的地址头；ssserver返回的HTTP返回报文标头，就可以通过已知密文 XOR 已知明文得到密钥流，进而就可以用伪造明文 XOR 密钥流得到伪造密文，诱使Shadowsocks暴露出来。如果这里方便理解，我们可以用与XOR等价的加法和减法进行叙述，以更好地说明问题：

已知明文 + 密钥流 = 已知密文

已知密文 - 已知明文 =密钥流

伪造明文 + 密钥流 =伪造密文

将其中的+和-替换成XOR即是：

已知明文 XOR 已知密钥流 = 已知密文

已知密文 XOR 已知明文 =密钥流

伪造明文 XOR 密钥流 =伪造密文

XOR也是满足交换律的。

而如何做到密钥流的一致？那就是初始向量IV的重复使用。由aes-256-cfb模式可知，前128比特密钥流完全是AES加密IV得到的；而Shadowsocks的IV是在数据流的最前方以明文形式直接发送的，早期并没有重用的校验，所以在伪造修改过的数据前面加上相同的IV，IV就会被Shadowsocks用于加密，就能得到一致的密钥流。

针对这类的探测攻击有两类，[^15]做了较为详尽的论述及实验，有兴趣的可以自行阅读。

精简来说，就是基于上述概念的已知明文攻击。我主要阅读了^16和[^17]，相对的理解了原理，在这里进行简要总结。

第一类攻击：针对ATYP字段

其中第一类攻击是针对sslocal向ssserver最先发送的，简化后的socks5请求头字段，即ATYP字段。在早期的Shadowsocks包括2.9.1中，发送的数据流在IV（一般是16个字节）后紧跟着就是这个裁剪过的socks5头，用于指明最终的目的服务器地址。

ATYP + address + port
+------+----------+-------+
| ATYP |  address |  port |
+------+----------+-------+
|  1B  | variable | u16be |
+------+----------+-------+

而ATYP正确有且只有三个字段：1（IPv4）、3（域名）、4（IPv6）。如果探测器截取了你的sslocal和ssserver通信的数据包，不修改IV，而修改密文重新发送，遍历数据的第17个字节，共2^8=256种可能，有1-3种情况会做出反应，如响应长度大于 0或超时。就可以断定服务器可能运行了Shadowsocks服务，被校园网管理员拉黑。

更进一步的是，管理员可以更有把握的是，他能锁定篡改的后的哪些值，你的ssserver可能会有反应，这会极大增强学校网管对判断正确的信心。它们分别是，其中有且只有：

• 原始密文 XOR 1 XOR 3
• 原始密文 XOR 3 XOR 4
• 原始密文 XOR 4 XOR 1

而且其中有且只有一个错误的。

如果难以理解，我们可以用之前的加法减法来说明，在学校网管截取的数据包中，第17位的原始明文应该是1或3或4（正确的类型），我们不妨设原始明文是3：

• 原始密文 XOR 1 XOR 原始明文
• 原始密文 XOR 原始明文 XOR 4
• 原始密文 XOR 4 XOR 1

就转换为：

• 原始密文 + 1 - 原始明文 = KEY + 1 = 1对应的加密密文
• 原始密文 - 原始明文 + 4 = KEY+4 = 4对应的加密密文
• 原始密文 + 4 + 1 = 错误的结果

其中KEY就是由IV生成的第一组密钥流。原始明文是1或者4也是如此，有着类似的轮换对称性，自己写出就明白了，这里就不写了。

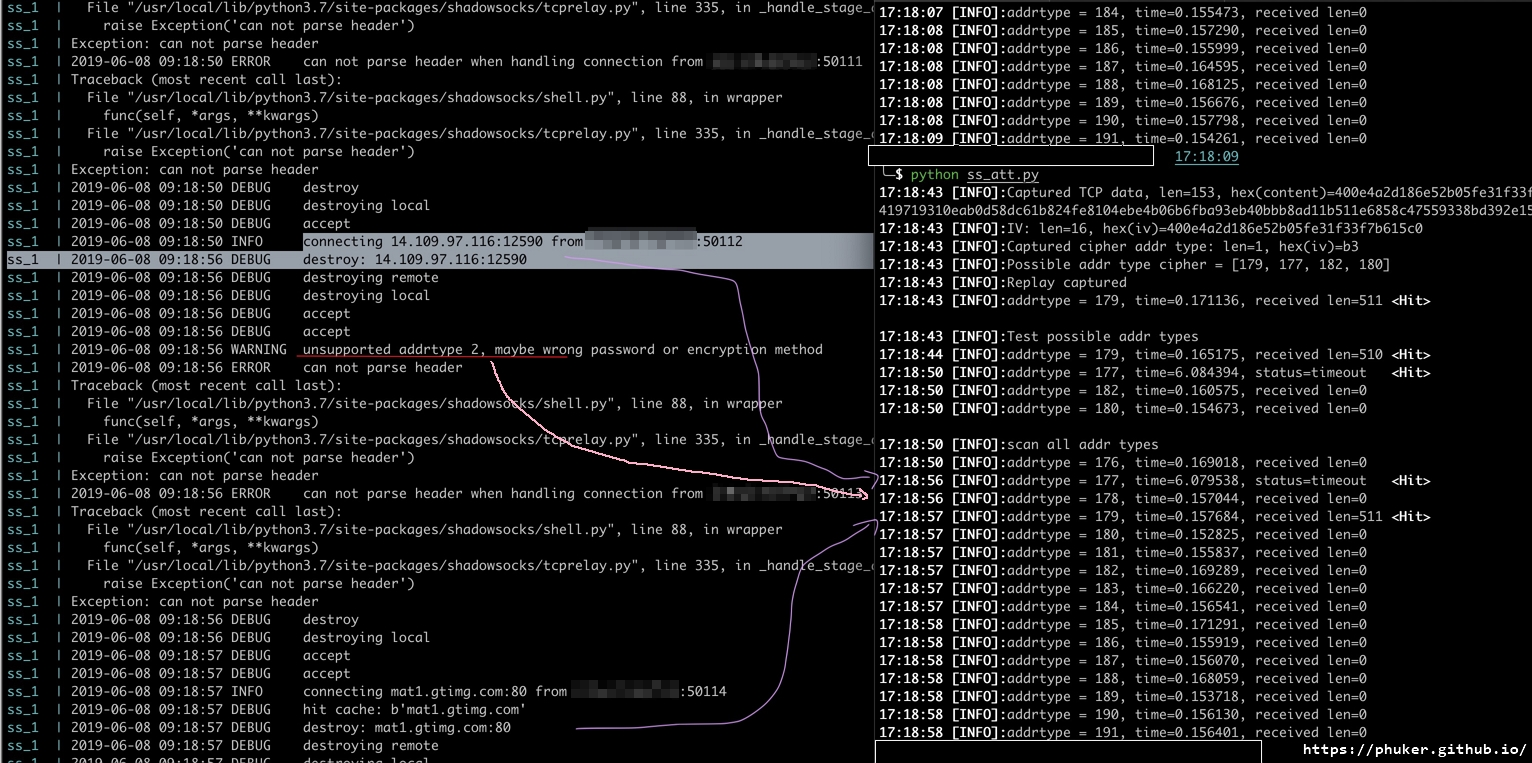
这样特征就变得更加明显，如果一个可疑对象当且仅当对这样的篡改后的数据包做出反应，就极有可能被封锁。如果对于上面的例子还不够清楚，我们就按照[^15]中的例子再做一个详细阐述，顺带总结一下Shadowsocks2.9.1对socks5连接阶段请求的处理。

在[^15]中，原始数据包IV后的第一个字节，ATYP的密文是0xb3，二进制是0b10110011；对应的明文是0x03，二进制是0b00000011，说明后面是一个主机名的格式。而博主原本访问的主机名是mat1.gtimg.com。

在修改密文为0b10110011 XOR 0b00000011 XOR 0b00000001(ipv4的标识)=0b10110001，也就是177（0xB1）后 ，ssserver会将后面的数据解析做ipv4地址，尝试连接，连接失败并作出timeout举动，即有反应。

在这里想记录的是，在修改密文后为什么，篡改后的数据包还会被处理成一个ipv4地址并出现连接超时的情况，而不是直接的解析失败，出现和其它的失败字段一样的结果。这里的核心问题就是Shadowsocks处理裁剪后socks5头的程序实现了。

    

​    
#common.py
def parse_header(data):
​    addrtype = ord(data[0])#返回Unicode 码点
​    dest_addr = None
​    dest_port = None
​    header_length = 0
​    if addrtype & ADDRTYPE_MASK == ADDRTYPE_IPV4:
​        if len(data) >= 7:
​            dest_addr = socket.inet_ntoa(data[1:5])#转为字符串

            dest_port = struct.unpack('>H', data[5:7])[0]#索引5/6的端口号
            header_length = 7
        else:
            logging.warn('header is too short')
    elif addrtype & ADDRTYPE_MASK == ADDRTYPE_HOST:
        if len(data) > 2:
            addrlen = ord(data[1])#取出地址长度
            if len(data) >= 4 + addrlen:
                dest_addr = data[2:2 + addrlen]
                dest_port = struct.unpack('>H', data[2 + addrlen:4 +
                                                     addrlen])[0]
                header_length = 4 + addrlen
            else:
                logging.warn('header is too short')
        else:
            logging.warn('header is too short')
    elif addrtype & ADDRTYPE_MASK == ADDRTYPE_IPV6:
        if len(data) >= 19:
            dest_addr = socket.inet_ntop(socket.AF_INET6, data[1:17])
            dest_port = struct.unpack('>H', data[17:19])[0]
            header_length = 19
        else:
            logging.warn('header is too short')
    else:
        logging.warn('unsupported addrtype %d, maybe wrong password or '
                     'encryption method' % addrtype)
    if dest_addr is None:
        return None
    return addrtype, to_bytes(dest_addr), dest_port, header_length

    

根据RFC1928，当ATYP为3时，目的地址是这样的格式：

+------+---------------------------+----------+
| ATYP |          DST.ADDR         | DST.PORT |
+------+---------------------------+----------+
|  1B  | length(1B)+主机名(varible) |    2B    |
+------+---------------------------+----------+

目的地址会先用1比特指示后面的主机名长度，而后是主机名。在[^15]的实验中，它原本访问的主机名是mat1.gtimg.com。

在这里DST.ADDR字段就会处理成14mat1.gtimg.com，其中14是第一个字节，后面的mat1.gtimg.com是ASCII码，一个字符占一个字节，那么逐字节处理

，以十进制展示，一个三个数字的数表示一个字节，就是014 109 097 116 049 046 103 116 105 109 103 046 099 111 109 013 010，按照上面的程序逻辑，dest_addr = socket.inet_ntoa(data[1:5])提取ip地址，就提取出了14.109.97.116，端口号就是49*2^8+46=12590，这就会导致ssserver尝试连接一个随机的ip+端口，导致出现超时错误，做出不一样的反应。这个结果也与原博主给出的图一致。三组可能值里的ipv6也是如此，就不一一分析了。

实际上，每个字节只能表示一个0-255的数，而ipv4地址是一个4字节的数，端口号是2字节的数，只是将ASCII编码当作原本的数进行处理了。

为了修正该问题，曾推出OTA方案。但是OTA方案，会出现固定位置的长度字段可能被篡改，导致ssserver一直等待后续的数据流，出现更明显的特征，现已废弃，详情请看[^5]。OTA的具体程序模块我也没看，只了解问题的原因和处理方案，不再赘述。

第二类攻击：针对ssserver可能向sslocal返回的HTTP头部（Header）字段

这是奇虎 360 核心安全团队（Qihoo 360 Core Security）提出的一个漏洞^16，本质上与第一类攻击一致，也是篡改密文。但不一样的是，第一类只是修改ATYP字段的值，第二类是直接构造ATYP、DST.ADDR、DST.PORT 字段，诱导ssserver发送明文数据到攻击者服务器。由于加解密方法的自恢复性，攻击者可以获得这个数据流后续的大部分明文。

这里仍以aes-256-cfb为例，如果是aes-256-cfb1或aes-256-cfb8反而就不行了，但是这两种加密方法由于其效率低下，AES加密一轮只生成1个或8个比特的密钥流，也基本没见人用过。

这种攻击成功有四个条件，从理论上我想进行详细的记录：

1. ssserver向sslocal返回的数据流格式是IV+服务器返回的数据流的密文，IV后直接跟着目标服务器返回的数据
2. sslocal向ssserver发送的数据流格式是IV+ATYP+DST.ADDR+DST.PORT，IV后直接跟着目标服务器的信息，用于ssserver确定数据转发目的地
3. CFB虽然当前密文会对部分后续密文的解密产生影响，但是当s=128时，前128比特密钥流仅由IV生成
4. IV的重用没有被处理

大多数通过Shadowsocks代理的流量，是浏览器的http访问，那么这些数据包中，目的服务器最先经过ssserver转发的数据流，大多就是HTTP/1.1。这就8个字节构成了已知明文攻击的条件：在IV固定的条件下，前16字节密钥流不变，前8字节明文和密文已知，就可以用来构造7字节的ipv4的ATYP+DST.ADDR+DST.PORT头部。我们取加减法来做公式的说明：

HTTP/1. + 前七字节密钥流 = 前七字节密文

HTTP/1. - 前七字节密文 = 前七字节密钥流

前七字节密钥流 + 伪造的ATYP+DST.ADDR+DST.PORT = 伪造的ATYP+DST.ADDR+DST.PORT密文

这样攻击者将原先数据流的IV后（一般是16字节）的7字节密文进行替换，就可以诱导ssserver向伪造的密文中对应的ipv4地址服务器发送数据。而aes-256-cfb中，128比特密文错误，只会造成接下来128比特解密错误，剩下的都会正常解密（后续用于AES加密的密文没有被篡改），这样攻击者就能获取到这条数据流大部分的信息（实际上是HTTP的返回报文），可以通过HTTP明文知道你访问的网站及一些相关信息。

基于这种方法，可以有一些其他类似的猜想完成已知明文攻击，[^15]有详细说明，以及作者的一些自己的想法。UDP不是这次学习过程中重点关注的，我也没看太细，这里着重于记录攻击的原理。

针对已知明文攻击的完善策略

这种流密码的形式（生成密钥流然后与明文XOR）很容易造到这种篡改密文的攻击。我自己认为有两种改进的方向：直接使用AES块密码方式加密或者采取带报文完整性的加密方法（仍可以是流密码）。块密码可以将密文的错误扩散到整块的解密；有消息完整性加密方法可以保证密文不被篡改。

直接用块密码加密，需要对数据完成填充，我也没有深入了解，可能实现起来也会影响效率。而目前主要的策略，就是更换成带报文完整性和鉴别性的加密方法，比如aes-256-gcm。虽然在SIP022中，要换成2022-blake3-aes-128-gcm 和2022-blake3-aes-256-gcm，这好像是和RFC8452[^18]相关的，但是我找不到哪里看到的了。RFC8452提供的aes-gcm加密方法对随机数的防误用有更好的表现，但是我没看完整文档，这里不做学习及记录。至于aes-256-gcm的学习，我主要详细阅读了NIST SP 800-38D的文档。对这种加密方式的了解，以该文档为基准进行后面的分析。

对于采用了带报文完整性加密方式的Shadowsocks，主要的分析学习基于[^19]，会在最后记录一些关于SIP022的学习体会。那么接下来按照简单记录GCM的加密方法，到如何应用到Shadowsocks，最后记录一点点SIP022的顺序展开。这里我只看了Shadowsocks2.9.1的程序，没有这部分相关的程序实现，故这里只是妄想和分析，准确性不能保证，仅用作学习感悟记录。如果有人看到，希望不要太当真，避免不必要的误导。

什么是GCM加密方法？

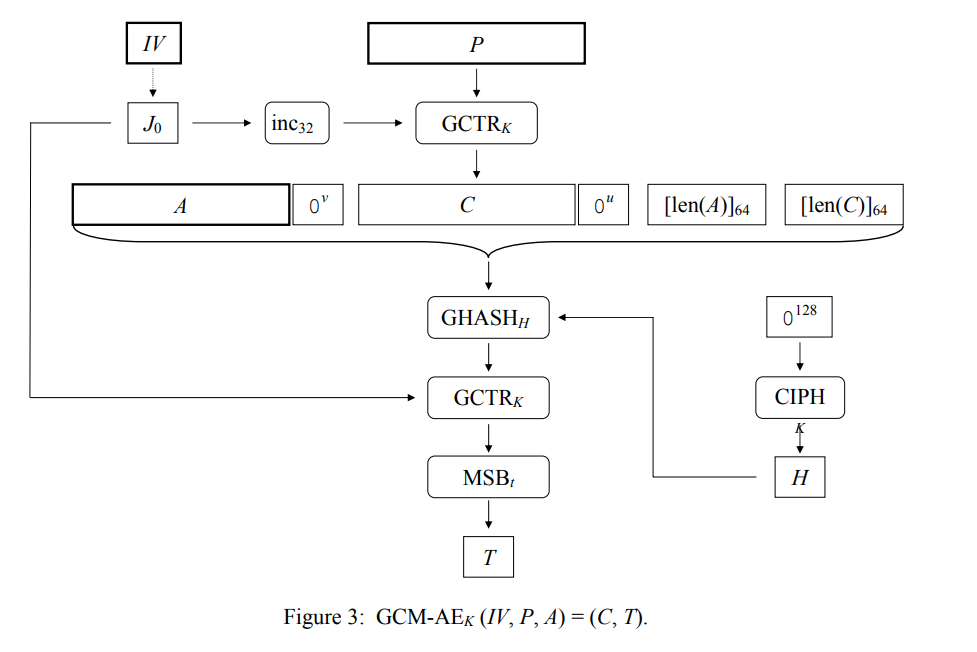
GCM（Galois/Counter Mode ）本质上是一种将计数器模式（CTR）（用于加密）和报文鉴别码（MAC）（用于报文完整性和鉴别性）结合起来的加密操作模式。底层的加密方法可以是多种，这里记录基于AES。GCM与CTR一样，可以加密任意长度的明文而不需要填充。

但GCM每次加密输出，除了和输入明文长度一致的密文，还有一个定长的tag（标签），用于确保报文完整性。解密时，需要输入密文和tag，才能解密出对应明文：

GCM_encrypt(key, IV, message,AD) => (ciphertext, tag)
GCM_decrypt(key, IV, ciphertext, tag,AD) => message

其中AD是关联数据（不需要加密的数据），Shadowsocks应该没有关联数据。

这种特性导致GCM加密方法是对长度敏感的，也就是GCM解密要正确提取密文块（以tag为分割，一般情况远大于底层AES的128比特），一并解密；而不能像CFB，收到一个字节数据可以解密一个字节，收到五个字节解密五个字节。如下文所示，密文是变长，tag是定长。需要将[密文][tag]作为一组用于解密操作。这里就涉及如何处理可变的密文长度，会在下一部分分析。这里先搁置。

[明文][明文][明文][明文]
  ↓
“加密操作”
  ↓
[密文][tag][密文][tag][密文][tag][密文][tag]

值得一提的是，GCM操作模式是AEAD类加密方法的一种。AEAD是Authenticated Encryption with Associated Data的缩写，翻译为“具有关联数据的身份验证加密”。AEAD是一类加密算法，同时提供加密和身份验证的功能，接受两个输入：明文数据（需要加密的数据）和关联数据（不需要加密的数据）。关联数据可以包括与主要数据相关的信息，例如时间戳、发送者/接收者标识、版本号或其他描述性信息。这些数据在解密时不会被加密，但它们参与了身份验证过程，确保解密的数据是完整和未被篡改的。而在Shadowsocks的GCM加密中，应该是没有关联数据的。

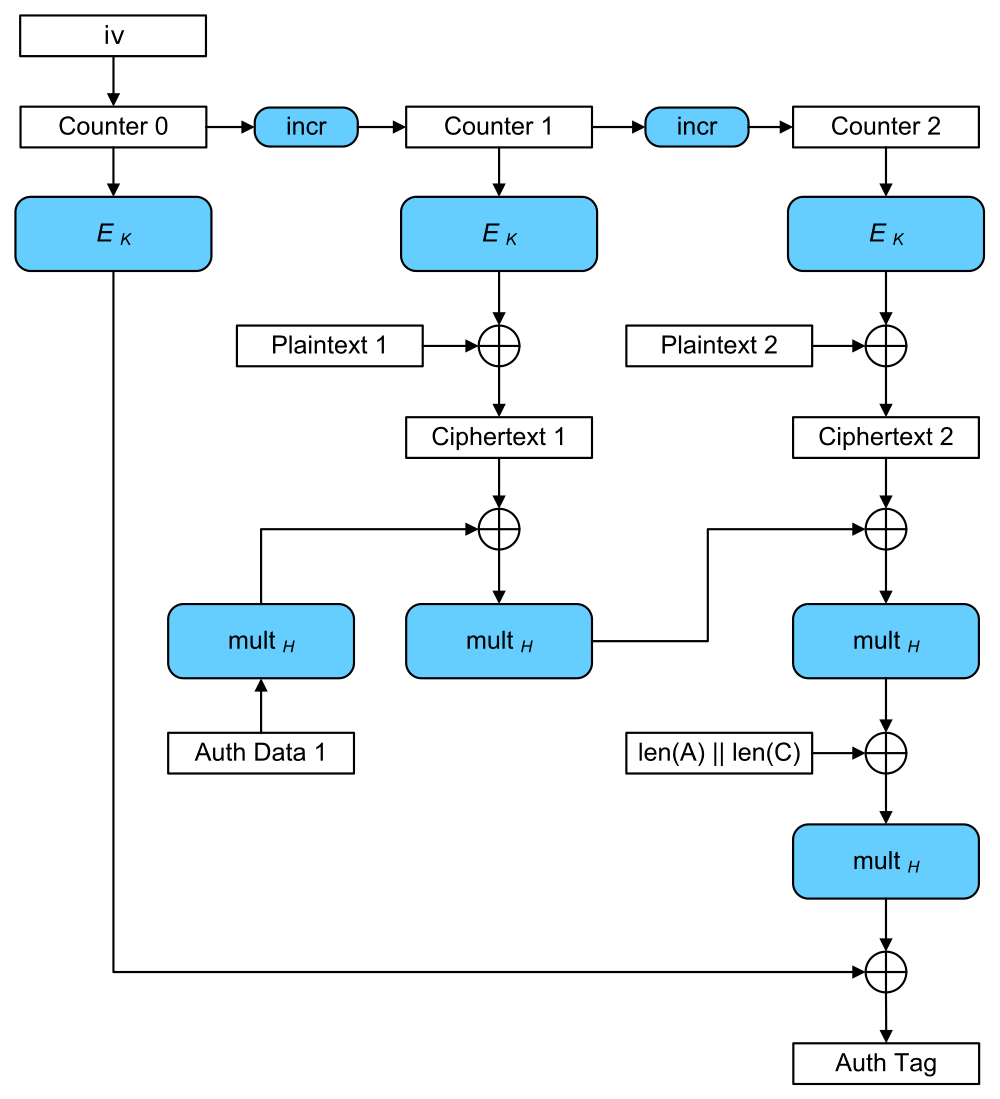
GCM的核心有有两个部分：加密和认证tag的生成。加密部分与CTR一致，由IV生成计数器（SP 800-38D），对计数器加密，与明文按位XOR运算得到密文。而认证tag的生成，则是涉及到tag的计算：在GF（2^128）上，对明文数据和关联数据各自补齐到128的整数倍，连同各自原本的长度，与一个被称为哈希子密钥（hash subkey）的128比特进行特定操作的乘法。接下来就详细说明一下tag的计算方法：

1. 获取hash子密钥，通过将底层加密方法（如AES）加密一个128位的0块（0^128）得到。
2. 明文数据C和关联数据A各自补齐到128的整数倍，连同各自的长度（用64位二进制串表示）连结起来，得到用于计算tag的比特串（长度是128的倍数）。
3. 按照GHASH的计算方法得到tag的中间值。
4. 对tag的中间值，用计数器初始值，使用底层方法加密（AES），取结果的左侧位数作为最终的输出tag。

至于第二步的比特串，需要按照如下得到：

𝑢=128∗⌈𝑙𝑒𝑛(𝐶)/128⌉−𝑙𝑒𝑛(𝐶),𝑣=128∗⌈𝑙𝑒𝑛(𝐴)/128⌉−𝑙𝑒𝑛(𝐴)，𝑢,𝑣代表C和A需要补齐到128整数倍需要的比特数，⌈ ⌉是向上取整。

用于计算tag中间值的比特串= A || 0^v || C || 0^u || [len(A)]_64 ||[len(C)]_64，其中||表示连接，0^u表示多少个0，[]表示转换为二进制形式，_64表示这是64位长度。

而第三步的GHASH的计算，则是将用于计算tag的比特串划分成128比特的m个块，X_1, X_2, ... , X_m-1, X_m，而后定义了Y_0=0^128，是一个128比特的全0比特串。然后计算Y_1,Y_2, ... , Y_m-1, Y_m，其中，Y_i = (Y_i-1 XOR X_i)*H，最终得到的Y_m就是GHASH的输出值。目前没处理公式的渲染，还是放个图好看。

本质上是X_1*H^m XOR X_2*H^m-1 XOR ..... XOR X_m-1*H^2 XOR X_m*H 。这也就解释了上面带蓝框那个图的Auth Tag的生成过程：mult_H表示用H作为参数的乘法（multiplication），关联数据与H做乘法，而后与每块密文与H做乘法的结果进行XOR运算，最后对长度块进行XOR运算。这样图就与公式描述一致了。wiki的这个图与SP 800-38D不同的是，SP 800-38D还将这个结果用初始计数块进行了底层（AES）加密，并取出了需要的长度作为最终的tag。但二者并不矛盾冲突，只是具体实现时的不同处理手段。

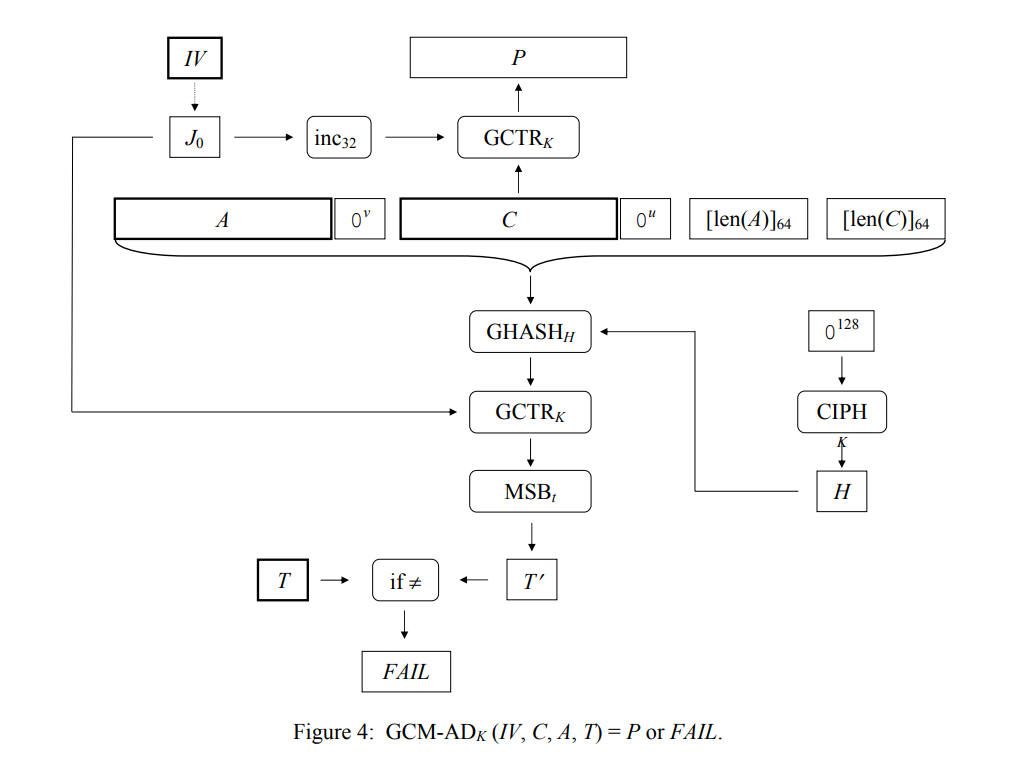
解密是类似的过程，按照IV生成计数器，用底层加密方法获得密钥流，XOR运算得到明文；对明文数据和关联数据用相同方法计算tag，验证计算出的tag与收到tag是否一致，不一致则返回fail，做异常处理。

将SP 800-38D的加密解密方法图拿过来用一下。

加密

解密

这里值得一说的是，IV生成的计数器，第一个计数块用于生成tag，第二个计数块才开始用于生成正文。而且SP 800-38D中，花了极大的篇幅，阐述在同一个密钥（KEY）（底层加密算法如AES用）下，IV绝对不能重复使用的重要性。

在作为这部分结束的部分，再次强调一下对几个加密解密所需参数的理解：

• key，密钥，用于底层的加密块算法。对于AES，则是用于派生“AddRoundKey”环节的每轮数据块。
• IV，初始向量，用于GCM操作模式，生成计数器，进而类似CTR模式对明文加密或解密，在一个key下不能重复使用。长度灵活，初始计数器还用于生成Hash subkey
• counter，计数器，由IV生成，用于类似于CTR完成加密解密过程，IV生成的counter初始值长度是128比特
• Hash subkey，哈希子密钥，由底层加密算法（使用key）加密一个全0的块得到，用于计算tag
• cipher，密文，由明文通过计数器加密得到，长度与明文一致
• plaintext，明文，长度与密文一致
• tag，标签，加密时生成的类似报文鉴别码的比特串，用于保证报文完整性和鉴别性，计算过程会用到哈希子密钥，tag长度是 128, 120, 112, 104, 96其中一个

顺带一提的是，GCM，如果只用来生成tag而不加密数据，这类技术被称作GMAC，直接退化成一种报文鉴别码。

现在还没来得及处理wordpress渲染LATEX，敲打的实在难看，这里有兴趣的朋友一定去读读原文。如何由IV得到计数器；各自符号运算的定义，都非常精确，读起来很有趣味。

Shadowsocks如何引入GCM加密方法

虽然依旧是直接对要中转的数据进行加密解密操作，但由于tag的存在，GCM类加密方法是对长度敏感的，不能直接的随来随加密，随来随解密。这里要进一步应用之前学习到的应用层设计准则：数据流被TCP协议层按序准确送到通信程序（Shadowsocks），我们需要做的是如何处理这个与发送端一致的数据流。那么在一次加密中可以加密任意长度的GCM操作模式，就需要完成一个流密码向类似块密码的转换：标识并处理密文长度。而GCM操作模式具有的密文和明文长度一致的特点，正好可以用来处理这个问题：用一个长度一定（比如8比特）的标识长度的“块”，来标识后续要中转的加密载荷的长度。

查阅Shadowsocks的相关文档，也确实可以发现这样的设计方法。但是为了尽可能消除特征，Shadowsocks采取了对标识长度的块也进行GCM加密的方法，以使数据流更随机，对学校网管可见度更差的做法。

[encrypted payload length][length tag][encrypted payload][payload tag]

其中payload length是一个2比特大端序无符号整数上限是0x3FFF，也就意味着encrypted payload的最大长度是2^14-1比特。举例来说，我们假设tag的长度是128比特。[length tag]是对length字段GCM加密后生成的tag。

为了方便理解，我们举这么一个例子：

[salt][encrypted payload1 length][length tag][encrypted payload1][payload1 tag][encrypted payload2 length][length tag][encrypted payload2][payload2 tag][encrypted payload3 length][length

这时候ssserver新建了一个TCPRelayHandler实例，并在第一次接收到如上的数据，但是这时TCPRelayHandler并不知道加密载荷的长度。其中salt是一个定长的随机数，假设16字节，用于AES加密密钥的生成，这里只需约定并知道这是一个定长数。并假设tag长度是96比特，12字节。按我个人理解，接下来就会发生以下事情

1. 首先读取前16字节，作为负责加解密Encryptor实例初始化的参数传入
2. 读取接下来的2+12字节，因为知道接下来该跟着2字节加了密的长度标识和12字节的tag，将其送入解密，解密得到载荷1的长度
3. 读取接下来的 载荷1长度+12字节，送入解密，得到第一部分载荷并处理
4. 读取接下来的2+12字节，解密得到载荷2的长度
5. 读取接下来的 载荷2长度+12字节，送入解密，得到第二部分载荷并处理
6. 读取接下来的2+12字节，发现长度不够，将其存入列表，等待后续数据流到达，再解密处理

这里[encrypted payload length]是定长的，它又会指代后续载荷的长度，可以让数据流有序的分割开并处理。类似于HTTP报文的长度字段；也类似于之前处理DNS报文时，每条资源记录的 RDLENGTH 字段；也类似于socks5协议，连接阶段，当ATYP=3，是域名时，主机名字段的第一个字节用于标识主机名的长度。这种设计方法和设计思想非常值得学习。它是基于TCP的可靠传输，将网络中不稳定的数据转换为可靠的数据流，然后在数据流之上切割处理的方式。

我曾经难以理解如何从流加密向这种长度敏感的类似块解密转变，但是学习过程中有了答案，之前也有提及了：加入判断语句。通过判断语句用长度判断整块的数据是否到达（GCM是加密数据+tag），到达则完成解密处理，未到达则存入缓存，等下一次读取后，拼接起来再行判断。

这里还要记录的是，Shadowsocks的aes-256-gcm与NIST SP800-38D有什么区别。

SP800-38D，多次强调在底层加密算法下，一个IV不能重复使用，每次加密都要换一个IV。

"In particular, if IVs are ever repeated for the GCM authenticated encryption function for a given key, then it is likely that an adversary will be able to determine the hash subkey from the resulting ciphertexts. The adversary could then easily construct a ciphertext forgery. Specifically, when provided with the ciphertext and tag outputs of an invocation of the authenticated encryption function, along with the associated IV and AAD inputs, the adversary could substitute any ciphertext and AAD strings and use the subkey to generate a valid substitute tag. Although this forgery would use the same IV, in most cases, it will not be feasible for the authenticated decryption function to detect the repetition. Thus, the assurance of authentication is essentially lost."

而早期的Shadowsocks中对AEAD的支持中，IV应该是不重数指代：(猜测不确定)

AE_encrypt(key, nonce, message) => (ciphertext, tag)
AE_decrypt(key, nonce, ciphertext, tag) => message

它是一个每次加密都从0开始的数，“The first AEAD encrypt/decrypt operation uses a counting nonce starting from 0. ”。这看似违反了nonce重用的问题，也难以理解每次加密和下一次加密时计数在连续性上的行为。而实际上这两个问题都得到了处理。

针对第一个问题，虽然每一个连接加密都用相同的不重数（从0开始，在一次块加密（AES）时，最后一位加1），但是每一次底层加密算法的主密钥是不同的，主密钥是通过输入的密码password和salt生成的，而salt是随机的，以明文发送，会在每个TCP/UDP连接改变，这也就保证了，在同一个key下，nonce不会被重用。下面语句是用来生成每个连接的子密钥（subkey）的表述。

HKDF_SHA1(key, salt, info) => subkey

而针对第二个问题，通过查看文档也可以发现是有说明的：每次加密/解密后，都会重置一个计数器，类似于SP 800-38D中的每次加密使用不同的IV的效果。这个加密解密是sslocal和ssserver约定好的，所以并不需要额外发送。

After each encrypt/decrypt operation, the nonce is incremented by one as if it were an unsigned little-endian integer.

具体来说，在每次加密和解密后，不重数就会像小端序递增1那样的增加。实际上就是会在数字高位增加1，来提供一个新的nonce来进行下一次加密。给一个详细的例子。加密长度块也是如此。

第一次的nonce 是阅读顺序，也是大端序，用于第一次加密，在不同块（AES）时，会在最后递增1
0b 10000000 00000000 00000000 00000000
按小端序+1，就是将第一个字节末尾+1 下一轮加密用这个nonce，起到了类似每次加密用不同IV的效果，在不同块（AES）时，会在最后递增1
0b 10000001 00000000 00000000 00000000

Note that each TCP chunk involves two AEAD encrypt/decrypt operation: one for the payload length, and one for the payload. Therefore each chunk increases the nonce twice.

以上是我对Shadowsocks如何引入AEAD算法，以AES-256-GCM为例，在程序设计上的一点想法。一没有阅读程序，也没有自己编写，就纯臆想，有人看的话请多思考，也希望屏幕前的你，可以帮我指出错误，共同进步。

SIP022的新特性

这里就记录几个自己有印象的点，作为收尾吧，具体的请大家移步原文档查看。我看的只有TCP部分，无UDP部分

一个是主密钥到子密钥的派生更为复杂：

session_subkey := blake3::derive_key(context: "shadowsocks 2022 session subkey", key_material: key + salt)

像Shadowsocks2.9.1这种md5不停滚动的方法，很容易被撞库破解，也早已淘汰了。

而且主密钥，也不能由password派生，而要有一定密码学安全性，直接生成的，固定长度的，主密钥。

二是进一步削弱sslocal向ssserver发送的数据流开始的特征：

+----------------+
|  length chunk  |
+----------------+
| u16 big-endian |
+----------------+

+---------------+
| payload chunk |
+---------------+
|   variable    |
+---------------+

Request stream:
+--------+------------------------+---------------------------+------------------------+---------------------------+---+
|  salt  | encrypted header chunk |  encrypted header chunk   | encrypted length chunk |  encrypted payload chunk  |...|
+--------+------------------------+---------------------------+------------------------+---------------------------+---+
| 16/32B |     11B + 16B tag      | variable length + 16B tag |  2B length + 16B tag   | variable length + 16B tag |...|
+--------+------------------------+---------------------------+------------------------+---------------------------+---+

Response stream:
+--------+------------------------+---------------------------+------------------------+---------------------------+---+
|  salt  | encrypted header chunk |  encrypted payload chunk  | encrypted length chunk |  encrypted payload chunk  |...|
+--------+------------------------+---------------------------+------------------------+---------------------------+---+
| 16/32B |    27/43B + 16B tag    | variable length + 16B tag |  2B length + 16B tag   | variable length + 16B tag |...|
+--------+------------------------+---------------------------+------------------------+---------------------------+---+

Request fixed-length header:
+------+------------------+--------+
| type |     timestamp    | length |
+------+------------------+--------+
|  1B  | u64be unix epoch |  u16be |
+------+------------------+--------+

Request variable-length header:
+------+----------+-------+----------------+----------+-----------------+
| ATYP |  address |  port | padding length |  padding | initial payload |
+------+----------+-------+----------------+----------+-----------------+
|  1B  | variable | u16be |     u16be      | variable |    variable     |
+------+----------+-------+----------------+----------+-----------------+

Response fixed-length header:
+------+------------------+----------------+--------+
| type |     timestamp    |  request salt  | length |
+------+------------------+----------------+--------+
|  1B  | u64be unix epoch |     16/32B     |  u16be |
+------+------------------+----------------+--------+

HeaderTypeClientStream = 0
HeaderTypeServerStream = 1
MinPaddingLength = 0
MaxPaddingLength = 900

在请求流开始时，多了两个固定的独立Header块，用于防止最初发给ssserver的只有ATYP+address+port，没有的载荷长度，而可能出现的定长特征。在这salt后紧跟着的这两个块，第一个块指示长度；第二个块可能承担载荷/也可能有填充，并且绝不能既没有载荷也没有填充。

三是增强了对重放攻击的抵抗：

在ssserver向sslocal和sslocal和ssserver发送的salt后第一个块，都在密文中添加了时间戳。程序实现会记录60s内的发送过来的salt值，解密后如果发现时间戳偏离超过30s，则当作异常处理；如果salt在60s内被重用，也会做异常处理。这增加了对重放攻击的抵抗能力。

心得

这一部分我以为没事想起什么记录点什么就行，结果篇幅远比我想象的要长。如果有人抱着想要了解一些SS加密的基础知识看到了这里，希望对你有所帮助。接下来还有几部分要记录。

However, I have been a uunemployed for half a year. It's imminent for me to find a job. Actually, I'm so proud of writting this part. It's not my major, even I haven't learn any about cryptography and network during my collage time. During writting time, I recall my senior high school times. Many useless concepts, I contacted when I was leisure during lessons, now shining in this blog. This tell me: even you cann't touch the core of a course, keep reading and thinking, when you next meet it, you could find the difference happens on you, even if you are still a fool.

[^1 ]: 计算机网络：自顶向下方法 第八章：计算机网络中的安全
[^2 ]: NIST SP 800-38D, Recommendationfor Block Cipher Modes of Operation: Galois/Counter Mode (GCM) and GMAC
[^3 ]: SIP022 AEAD-2022 Ciphers | Shadowsocks
[^4 ]: Student Resources | Kurose/Ross, Computer Networking: a Top-Down Approach, 7/e (pearsoncmg.com)
[^5 ]: 为何 shadowsocks 要弃用一次性验证 (OTA) - PRIN BLOG (prinsss.github.io)
[^6 ]: 从零实现 AES 加密算法 (sxyz.blog)
[^7]: Advanced Encryption Standard - Wikipedia
[^8 ]: Block Cipher modes of Operation - GeeksforGeeks
[^9 ]: 在 RSA 加密中既然公钥和私钥是可逆的，为什么都是把公钥给别人，而不把私钥给别人，自己保存好公钥？ - V2EX
[^10]: 为什么不应该用 SSL 翻墙 (github.com)

[^11]: Shodowsocks不同加密方式速度区别 · openwrt-fanqiang (gitbooks.io)
[^12]: 应用密码学 协议、算法与C源程序（原书第二版）P140

[^14]: 伽罗华域(Galois Field，GF)乘法运算_gf域运算-CSDN博客
[^15]: 使用主动探测方法识别 Shadowsocks 服务 - Phuker's Blog

[^17]: edwardzpeng/shadowsocks: Redirect attack on Shadowsocks stream ciphers (github.com)
[^18 ]: RFC 8452: AES-GCM-SIV: Nonce Misuse-Resistant Authenticated Encryption (rfc-editor.org)
[^19]: AEAD ciphers | Shadowsocks